Prawdopodobieństwo sprawdzenie zadania Radek: Witam mam takie zadanie W szufladzie jest para niebieskich rękawiczek oraz para czerwonych.Doświadczenie losowe polega na wyjęciu z szuflady jednej rękawiczki, odłożeniu jej na bok, a następnie wyjęciu drugiej rękawiczki.Oblicz prawdopodobieństwo, że: a)obie rękawiczki będą jednakowego koloru b)obie rękawiczki będą różnego koloru i prosiłbym o sprawdzenie a) Ω=4*3=12 a)|A|=2*1+2*1=4 P(A)=⁴₁₂=¹₃ b)B' obie rękawiczki są takiego samego koloru P(B)=1−¹₃=²₃ Czy zadanie są dobrze wykonane ? Dziękuje

PW: Ni diabła nie wiem jak sprawdzić, brak konstrukcji (opisu) przestrzeni zdarzeń. Sądząc z zapisu |Ω|=4•3 ustawiasz te rękawiczki w parę uporządkowaną − chyba jest to złe podejście (nie ma znaczenia, czy wyciągnąłeś "lewą czerwoną i prawą niebieską", czy "lewą niebieską i prawą czerwoną"). Niech Cię nie cieszy wynik liczbowy, zadanie jest źle rozwiązane.

PW: Nie stresuj się, to żart. Poważnie traktuj uwagę o konieczności opisu przestrzeni zdarzeń. Mówiąc dalej poważnie rozwiązałbym tak: Zdarzeniami elementarnymi są dwuelementowe podzbiory zbioru czteroelementowego. Jest ich niewiele, więc wypiszmy: Ω = {{n₁,n₂}, {c₁,c₂}, {c₁,n₁}, {c₂,n₁}, {c₁,n₂}, {c₂,n₂}} Są to dwuelementowe zbiory, kolejność wypisywania elementów nie ma znaczenia. W zadaniu mówiono o kolejnym losowaniu dwóch przedmiotów, ale z opisu wynika, że równie dobrze można wylosować oba jednym ruchem (nie zwracamy pierwszego przedmiotu, a interesują nas tylko kolory − nie kolejność wylosowania). |Ω|=6 Zdarzenie A − "obie wylosowane rękawiczki są jednakowego koloru" ma dwa elementy: A = {{n₁,n₂}, {c₁,c₂}} Uwaga: tu znowu kolejność wypisywania elementów nie ma znaczenia, interesuje nas przecież tylko to, czy obie rękawiczki są niebieskie lub obie czerwone, a więc rozpatrujemy dwuelementowe podzbiory, a nie uporządkowane pary. |A| = 2 Przyjmujemy, że każde zdarzenie jest jednakowo prawdopodobne, więc na mocy twierdzenia zwanego klasyczną definicją prawdopodobieństwa

	|A|		2		1
P(A) =		=		=
	|Ω|		6		3

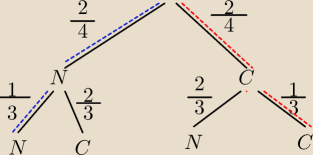
Mila: a)A− obie rękawiczki będą jednakowego koloru

	2		1		2		1		2		1
P(A)=		*		+		*		=		=
	4		3		4		3		6		3

b)B− obie rękawiczki będą różnego koloru

	2		2		2		2		8		2
P(B)=		*		+		*		=		=
	4		3		4		3		12		3

PW: Mila, teraz to adept probabilistyki będzie miał prawdziwy mętlik w głowie − trzecie poprawne rozwiązanie. Jest to jednak sposób trudny, tak naprawdę wzór Bayesa .

Mila: Niech żyją drzewa!

PW: I jeszcze "reguła mnożenia", cokolwiek by to miało znaczyć.