fiza Theosh: Fizyka −−−−−> kinematyka Ciało porusza się ruchem jednostajnie przyspieszonym, przebywając kolejno dwa równe odcinki drogi s = 15m w czasach t₁ = = 2s i t₂ = 2s. Znajdź prędkość ciała na końcu pierwszego odcinka i przyspieszenie a. Po dłuższym namyśle skołowałem to:

	1
s = v1t1 +		at12
	2

	1
s = (v1 = at1)t2 +		at22
	2

Odpowiedzi:

	2s(t1−t−2)
a =
	t1t2(t1+t2)

	s(2t1t2 +t22 − t12)
v1 =
	t1t2(t1+t2)

Problem mam z tym jak przekształcić te wzory do podanych powyżej.

Piotr 10: Trochę to sensu nie ma, na pewno dane dobrze przepisane?

Piotr 10: Ogólne myślenie jest ok. Tylko na pewno t₁=t₂

Theosh: Przepraszam. t₂ = 1s. tam w drugim s w nawiasie powinno być s=( v₁ + at₁)...

	2s(t1 − t2
a=
	t1t2(t1 + t2)

Poza tym dobrze przepisałem. Sorka.

Theosh: Możesz pi dać wskazówki jak przekształcić te wzory do odpowiedzi?

Piotr 10: Ja muszę już iść, na pewno ktoś inny z forum Ci pomoże

Theosh: ok.

Theosh: ?

Trivial: Licząc z odpowiedzi masz: a = 5 m/s² v₁ = 2.5 m/s Sprawdźmy to. s = v₁t₁ − ¹₂at₁² 15 = 5 − 0.5*5*4 // oczywista nieprawda Wygląda na to, że podali odpowiedź na v₀, a nie v₁.

Sławek: Tam jest ruchem jednostajnie przyspieszony, s = v₁t₁ + ¹₂at₁²

Trivial: Sławek dałeś się nabrać. v₁ to prędkość końcowa po przebyciu pierwszego odcinka, a nie początkowa (tę oznaczyłem v₀).

Sławek:

Trivial: W zadaniu pytają o prędkość po przebyciu pierwszego odcinka (v₁), a potem w odpowiedzi podają v₀ − prędkość na początku pierwszego odcinka.

Theosh: Dobra może przepiszę treść dokładnie tak jak jest w książce. Ciało porusza się ruchem jednostajnie przyspieszonym, przebywając kolejno dwa równe odcinki drogi s = 15 m w czasach t₁ = 2s i t₂ = 1s. Znaleźć przyspieszenie ciała a i prędkość na początku pierwszego odcinka.

Theosh: Przepraszam za błąd o 16.07. Prędkość na końcu pierwszego odcinka to v₁ + at₁. Pisząc treść zadania się zamyśliłem. Myślę co innego i piszę co innego

Trivial: W takim razie sprawa jest bardzo prosta. Trzeba rozwiązać układ równań:

⎧	s = v0t1 + 12at12
⎩	2s = v0(t1+t2) + 12a(t1+t2)2

Łatwo to można zrobić wyznacznikami.

Theosh: Jak myślisz zadania tego pokroju mogą być na maturze poz. rozszerzony czy za wysokie loty ?

Trivial: Przecież to prościutkie zadanko. Trzeba tylko podstawić do wzoru i rozwiązać układ dwóch równań liniowych. Moim zdaniem spokojnie mogłoby się na rozszerzeniu pojawić.

Theosh:

	1		1
2(v0t1 +		at12) = v0(t1+t2) +		a(t1+t2)2?
	2		2

Trivial: Tak, ale to nic nie daje. Wystarczy policzyć 3 wyznaczniki i już. W = ¹₂t₁(t₁+t₂)² − ¹₂t₁²(t₁+t₂) = ¹₂t₁t₂(t₁+t₂) W_v0 = ¹₂s(t₁+t₂)² − st₁² = ¹₂s(2t₁t₂+t₂²−t₁²) W_a = 2st₁ − s(t₁+t₂) = s(t₁−t₁)

	s(2t1t2+t22−t12)
v0 =
	t1t2(t1+t2)

	2s(t1−t2)
a =
	t1t2(t1+t2)

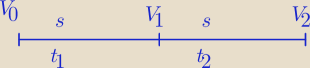
daras: S=V₀t₁+^at₁2₂ S=V₁t₂+^at₂2₂ po podstawieniu do drugiego r−nia: v₁=v₀+at₁ mamy 2 niewiadome: V₀ i a wyznaczamy przyspieszenie z pierwszego r−nia: a=^{2(s−v₀t₁)}_t1² i podstawiamy do drugiego otrzymując v₀=^{s(t₂2+2t₁t₂−t₁2)}_t1t2(t1+t2) = = ¹⁵₆ ^m_s a wracając do wyznaczonego wcześniej przyspieszenia dostajemy a = 5 ^m_s²

daras: nie wiem czemu ułamki wyszły mi takie niewyraźne, sorry