zada new: w kule wpisano dwa stozki o wspolnej podstawie z ktorej jeden ma pole powierzchni bocznej 3 razy wieksze niz drugi oblicz stosunek wysokosci tych stozkow

new: w trojkat o boku dl.a i katach ostrych do niego przyleglych o miarach β i γ obraca sie dookola prostej rownoleglej do tego boku poprowadzonej prez wierzcholki kata do niego przeciwleglego oblicz V powstalej bryly

new: takie dwa cuda

AROB: Pomogę

new: dzeki AROB

AROB:

	h1
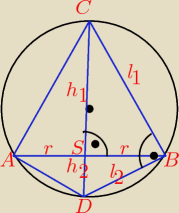
Zad. 1. Pb1 = 3Pb2 obl.
	h2

P_b1 = πrl₁ , P_b2 = πrl₂ Czyli: πrl₁ = 3πrl₂ ⇒ l₁ = 3l₂ ΔBCD ∼ ΔCSD

	r		l2
Stąd:		=
	h1		l1

	r		l2
		=		⇒ h1 = 3r
	h1		3l2

ΔBCD∼ΔSDB

	r		l1
Stąd:		=
	h2		l2

	r		3l2		r
		=		⇒ h2 =
	h2		l2		3

	h1		3r		3
		=		= 3r *		= 9
	h2		r   3		r

AROB: Zad. 2. Robi się.

new: spoko nie pospieszam dzieki

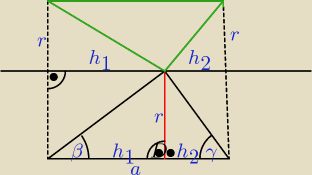AROB: Dane: a, β, γ V = ?

	1		1
V = Vw − (V1 + V2) = πr2a − (		πr2h1 +		πr2h2} =
	3		3

	1
a = h1 + h2 = πr2a −		πr2(h1 + h2) =
	3

	1		2
h1= a − h2 = πr2a −		πr2a =		πr2a
	3		3

r
	= tgβ ⇒ r = h1tgβ
h1

r
	= tgγ ⇒ r = h2tgγ
h2

Czyli z porównania: h₁tgβ = h₂tgγ (a − h₂)tgβ = h₂tgγ atgβ − h₂tgβ − h₂tgγ = 0

	atgβ
h2(tgβ + tgγ) = atgβ ⇒ h2 =
	tgβ + tgγ

	atgβ*tgγ
Zatem: r =
	tgβ + tgγ

Obliczony promień r podstawiamy do objętości:

	2		atgβ * tgγ		2a2πtgβ *tgγ
V =		πa *		=
	3		tgβ + tgγ		3(tgβ + tgγ)

new: wow dzieki

AROB: