w trójkącie ami: W trójkącie prostokątnym o przyprostokątnych 3cm i 4cm poprowadzono wysokość z wierzchołka kąta prostego. Oblicz długości odcinków,na jakie podzieliła przeciwprostokątną.

wredulus: Krok 1 obliczasz przeciwprostokatna wyjsciowegi trojkata Krok 2 obliczasz wysokosc poprowadzona z kata prostego Krok 3 z tw. Pitagorasa obliczasz dlugosci tych odcinkow Koooniec

ami: wyszło mi c=5

wredulus_pospolitus: bardzo dobrze −−− w końcu jest to 'trójkąt Pitagorasa'

ami: jak obliczyc wysokość ze wzoru na pole trójkata

wredulus_pospolitus: tak ... ze wzoru na pole

ami: możesz mi pomóc jakos mi dalej nie idzie.

wredulus_pospolitus:

	3*4
Pt =		= ....
	2

	5*h
Pt =		= ....
	2

wyznacz 'h'

ami: wyszło mi h=2 u {2} {5}

ami: 2u{2} {5}

wredulus_pospolitus: bez spacji pomiędzy }{ ... i duże U

	2
2
	5

no dobrze ... to teraz 'lecisz' do kroku 3

gość:

	2		12		144
CZYLI;a2+b2=c2 ,a2+(2		)2=32,a2=9−(		)2.a2=9−		coś nie tak w
	5		5		5

odpowiedzi mam 1,8 i 3,2 gdzie bład

wredulus_pospolitus:

	144
a2 = 9 −		= ...
	25

i z tego pierwiastek

gość: a= 9 dlaczego inaczej niz w książce

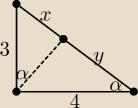
Bogdan: można bez obliczania wysokości: x + y = √3² + 4² = 5

x		3
	=		⇒ x = ...
3		5

y		4
	=		⇒ y = ...
4		5

ICSP:

	144		225		144		81
a2 = 9 −		=		−		=
	25		25		25		25

	81		9
skoro a2 =		oraz a > 0 to a =
	25		5