graniastosłup kika: Graniastosłup prawidłowy czworokątny przecięto płaszczyzną przez krawędź boczną, przekątnąpodstawy o długości 6√2 pole przekroju jest równe 72√3cm². Oblicz miarę kąta nachylenia przekątnej graniastosłupa do płaszczyzny podstawy oraz pole powierzchni całkowitej i objętość...

AROB: Pomagam

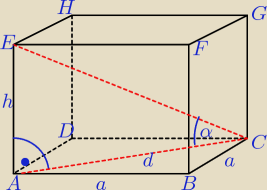
AROB: Dane: d= 6√2 cm P_ACGE = 72√3 cm² α, P_c, V = ? P_ACGE = dh

	72√3		72√6
6√2 * h = 72√3 ⇒ h =		=		= 6√6
	6√2		12

	h
Z ΔEAC obl. kąt α:		= tgα
	d

	6√6
tgα =		= √3 ⇒ α = 600
	6√2

d = a√2 , czyli a√2 = 6√2 ⇒ a = 6 cm P_C = 2a² + 4ah Podstaw i otrzymasz P_c = 72 + 144√6 = 72(1 + 2√6) [cm²] V = a²h Podstaw i otrzymasz: V = 216√6 [cm³]