Janek191:
A = ( − 5; − 1)
2x − 3y − 6 = 0 ⇒ 3y = 2x − 6 ⇒ y =
23 x − 2
23*a
2 = − 1 ⇒ a
2 = −
32
więc dowolna prosta prostopadła do danej będzie miała równanie
y = −u{3}[2} x + b
2
Ma ona przechodzić przez punkt A = ( − 5; − 1) , więc
− 1 = −
32*(−5) + b
2
− 1 −
152 = b
2
b
2 = −
172
y = −
32 x −
172
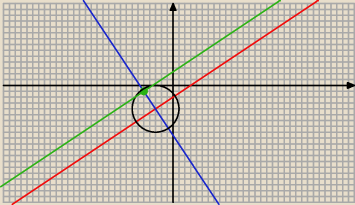
Te dwie proste przecinają się w punkcie, który jest środkiem okręgu
y =
23 x − 2
y = −
32 x −
172
zatem
23 x − 2 = −
32 x −
172 / * 6
4 x − 12 = − 9x − 51
4x + 9x = 12 − 51
13 x = − 39
x = − 3
=====
y =
23*(−3) − 2 = − 2 − 2 = − 4
−−−−−−−−−−−−−−−−−−−−−−−
więc
S = ( − 3; − 4 )
oraz
I AS I = r ⇒ r
2 = I AS I
2 = ( − 3 −(−5))
2 + (− 4 − (−1))
2 = 2
2 + (−3)
2 = 4 + 9 = 13
a) Równanie okręgu :
( x + 3)
2 + ( y + 4)
2 = 13
=======================
b) Styczna do okręgu w punkcie A = ( −5; − 1) to prosta równoległa do prostej
o równaniu y =
23 x − 2
zatem
y =
23x + b
3
− 1 =
23*( − 5) + b
3
− 1 = −
103 + b
3
b
3 =
103 −
33 =
73
y =
23 x +
73
==================
 A = ( − 5; − 1)
2x − 3y − 6 = 0 ⇒ 3y = 2x − 6 ⇒ y = 23 x − 2
23*a2 = − 1 ⇒ a2 = −32
więc dowolna prosta prostopadła do danej będzie miała równanie
y = −u{3}[2} x + b2
Ma ona przechodzić przez punkt A = ( − 5; − 1) , więc
− 1 = −32*(−5) + b2
− 1 − 152 = b2
b2 = −172
y = − 32 x − 172
Te dwie proste przecinają się w punkcie, który jest środkiem okręgu
y = 23 x − 2
y = −32 x − 172
zatem
23 x − 2 = −32 x − 172 / * 6
4 x − 12 = − 9x − 51
4x + 9x = 12 − 51
13 x = − 39
x = − 3
=====
y = 23*(−3) − 2 = − 2 − 2 = − 4
−−−−−−−−−−−−−−−−−−−−−−−
więc
S = ( − 3; − 4 )
oraz
I AS I = r ⇒ r2 = I AS I2 = ( − 3 −(−5))2 + (− 4 − (−1))2 = 22 + (−3)2 = 4 + 9 = 13
a) Równanie okręgu :
( x + 3)2 + ( y + 4)2 = 13
=======================
b) Styczna do okręgu w punkcie A = ( −5; − 1) to prosta równoległa do prostej
o równaniu y = 23 x − 2
zatem
y = 23x + b3
− 1 = 23*( − 5) + b3
− 1 = − 103 + b3
b3 = 103 − 33 = 73
y = 23 x + 73
==================
A = ( − 5; − 1)
2x − 3y − 6 = 0 ⇒ 3y = 2x − 6 ⇒ y = 23 x − 2
23*a2 = − 1 ⇒ a2 = −32
więc dowolna prosta prostopadła do danej będzie miała równanie
y = −u{3}[2} x + b2
Ma ona przechodzić przez punkt A = ( − 5; − 1) , więc
− 1 = −32*(−5) + b2
− 1 − 152 = b2
b2 = −172
y = − 32 x − 172
Te dwie proste przecinają się w punkcie, który jest środkiem okręgu
y = 23 x − 2
y = −32 x − 172
zatem
23 x − 2 = −32 x − 172 / * 6
4 x − 12 = − 9x − 51
4x + 9x = 12 − 51
13 x = − 39
x = − 3
=====
y = 23*(−3) − 2 = − 2 − 2 = − 4
−−−−−−−−−−−−−−−−−−−−−−−
więc
S = ( − 3; − 4 )
oraz
I AS I = r ⇒ r2 = I AS I2 = ( − 3 −(−5))2 + (− 4 − (−1))2 = 22 + (−3)2 = 4 + 9 = 13
a) Równanie okręgu :
( x + 3)2 + ( y + 4)2 = 13
=======================
b) Styczna do okręgu w punkcie A = ( −5; − 1) to prosta równoległa do prostej
o równaniu y = 23 x − 2
zatem
y = 23x + b3
− 1 = 23*( − 5) + b3
− 1 = − 103 + b3
b3 = 103 − 33 = 73
y = 23 x + 73
==================