wektory zadanie: znajdz rzut prostopadly do wektora [1,2] na os wyznaczona przez wektor [2,1] prosze o pomoc

zadanie: ?

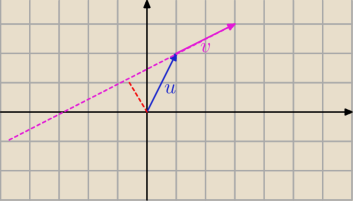
Mila: Znajdz rzut prostopadly wektora u^→ [1,2] na oś wyznaczoną przez wektor v^→ [2,1] 1) normalizujemy wektor v^→ |v|=√5

	2		1
vn=[		,		]
	√5		√5

2) Mnożymy

	2		1		2		2		4
vn→◯u→[		,		]◯[1,2]=		+		=
	√5		√5		√5		√5		√5

3) mnożymy v_n przez otrzymana wartość

	4		2		1		8		4
urz→=		*[		,		]=[		,		] wektor po rzutowaniu.
	√5		√5		√5		√5		√5

II sposób wzory

	u→◯v→
d=
	|v|

	v→
urz→=		*d
	|v|

zadanie: dziekuje

zadanie: Wykorzystując wyznacznik rozstrzygnij czy punkty A=(1,−1), B=(3,3), C=(13,23) sa współliniowe. jakies podpowiedzi?

PW: u^→[a,b] i V^→=[c,d] są współliniowe ⇔ mają proporcjonalne współrzędne (jeden z nich jest wielokrotnością drugiego) ⇔ istnieje liczba k, taka że [a,b]=k[c,d] ⇔ [a,b] = [ka,kb] ⇔

	a b ka kb		a b c d
		= 0 ⇔		= 0

(te nawiasy zamiast kresek oznaczających wyznacznik, bo w tym edytorze chyba sie nie da).

PW: To tylko podpowiedź, ale przy rozważaniu ogólnym powinienem raczej napisać "równoległe" zamiast "współliniowe" − wiesz, o co idzie?

zadanie: tzn. my mielismy wyznacznik typu det(u,v) a wtedy jak?

zadanie: a moge zrobic tak: AB=[2,4] AC=[12,24] det(AB, AC)=48−48=0 czyli punkty A, B, C sa wspolliniowe? dobrze

zadanie: prosilbym o sprawdzenie tego zadania

zadanie: dane sa dwa wierzcholki rownolegloboku A(2,5) i B(5,1) oraz jego pole s=17. wyznaczyc wspolrzedne dwoch pozostalych wierzcholkow wiedzac, ze punkt przeciecia przekatnych znajduje sie na osi Oy. wiem, ze: det(bd,ba)=17 a dalej? jakies podpowiedzi?

zadanie: ?

Mila: 1) zrób rysunek. S=(0,y)

	1
PΔSAB=		*17
	4

SA^→=[2,5−y] SB^→=[5,1−y] ułóż równanie, po obliczeniu wsp. punktu S łatwo wyznaczysz wsp. C i D

zadanie: ok dziekuje a moge prosic o sprawdzenie zadania z godziny 15:56 ?

Mila: Punkty są współliniowe. Metoda bez wyznacznika to potwierdza. Prosta AB: y=2x−3

PW: Jeżeli używacie wyznacznika pary wektorów, to powinno być powiedziane, żę zerowanie się wyznacznika oznacza równoległość wektorów (usiłowałem to pokazać). W tym wypadku wektory mają wspólny początek, czyli ich początek i końce są współliniowe. A znasz związek między wyznacznikiem a polem trójkąta?

Mila: Z tego co pisze autor wynika, że ma to podane na wykładzie ( ćwiczeniach). Ja to sprawdzam tradycyjnie , prosta i ...