dwie wartości bezwzględne
Bartek123: Proszę o rozwiązanie
||x+1|−2|=x−1
16 paź 20:13
16 paź 20:15
Bartek123: W taki sam sposób robiłem jednak wynik wychodzi mi inny niż z tyłu książki

mógłbym prosić
kogoś o rozpisanie tego przykładu?
16 paź 20:33
Bartek123: wychodzi mi x≥−1 w a powinno wyjsć x≥1
16 paź 20:46
Mila:
D:
x−1≥0⇔x>1 bo ||x+1|−2|≥0
||x+1|−2|=x−1
1
o
|x+1|=x+1 dla x≥−1
wtedy mamy równanie:
|x+1−2|=x−1⇔|x−1|=x−1
|x−1|=x−1 dla x≥1
x−1=x−1
−1=−1 zachodzi dla każdego x≥1
|x−1|=−x+1 dla x<1 przedział nie należy do dziedziny
2
o
|x+1|=−x−1 dla x<−1 przedział nie należy do dziedziny równania
odp.
x∊<1,
∞)
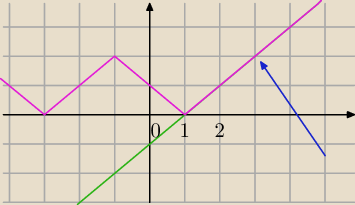
Graficznie:
f(x)=||x+1|−2|
g(x)=x−1
16 paź 21:30
 mógłbym prosić
kogoś o rozpisanie tego przykładu?
mógłbym prosić
kogoś o rozpisanie tego przykładu?
 D: x−1≥0⇔x>1 bo ||x+1|−2|≥0
||x+1|−2|=x−1
1o
|x+1|=x+1 dla x≥−1
wtedy mamy równanie:
|x+1−2|=x−1⇔|x−1|=x−1
|x−1|=x−1 dla x≥1
x−1=x−1
−1=−1 zachodzi dla każdego x≥1
|x−1|=−x+1 dla x<1 przedział nie należy do dziedziny
2o
|x+1|=−x−1 dla x<−1 przedział nie należy do dziedziny równania
odp.
x∊<1,∞)
Graficznie:
f(x)=||x+1|−2|
g(x)=x−1
D: x−1≥0⇔x>1 bo ||x+1|−2|≥0
||x+1|−2|=x−1
1o
|x+1|=x+1 dla x≥−1
wtedy mamy równanie:
|x+1−2|=x−1⇔|x−1|=x−1
|x−1|=x−1 dla x≥1
x−1=x−1
−1=−1 zachodzi dla każdego x≥1
|x−1|=−x+1 dla x<1 przedział nie należy do dziedziny
2o
|x+1|=−x−1 dla x<−1 przedział nie należy do dziedziny równania
odp.
x∊<1,∞)
Graficznie:
f(x)=||x+1|−2|
g(x)=x−1