Trudne, ciekawe zadanie z wartościami trygonometrycznymi Sebastian: Znajdź dwa rozwiązania równania

	cosx		π		π
tgx+		=2 x∊(−		,		)
	1+sinx		2		2

	sinx		1
Jedno rozwiązanie mi wyszło gdy za tgx podstawiłem		i wychodzi potem cosx=
	cosx		2

A drugie nie wiem jak zrobić, żeby wyszło, a wiem że na pewno są dwa rozwiązania, proszę o pomoc

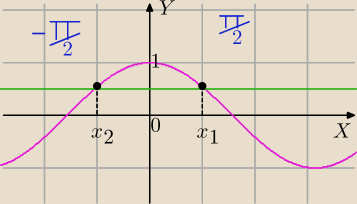Mila: 1+sinx≠0⇔sinx≠−1 x≠π

sinx		cosx
	+		=2
cosx		1+sinx

sinx*(1+sinx)+cos2x
	=2
cosx*(1+sinx)

sinx+sin2x+cos2x
	=2⇔
cosx*(1+sinx)

1
	=2
cosx

	1
cosx=
	2

	π		π
x=		lub x=
	3		3

Sebastian: a rzeczywiście ! Ale jestem głupi, zapomniałem o okresowości i to że mogą być dwa rozwiązania, w takim razie przepraszam za moją nie uwagę I dziękuję oczywiście Mila

Mila: Teraz będziesz lepiej o tym pamiętał.

Mila: Oczywiście pominęłam znak .

	π		π
x=		lub x=−
	3		3