Trójkąty, okręgi i trygonometria..
Fasola022: 1. W Δ prostokątnym cos jednego z kątów ostrych wynosi 0,8. Promień okręgu wpisanego w ten Δ ma
długość 9cm. Oblicz pole tego trójkąta.
2. Pole Δ wynosi 336, a promień okręgu wpisanego w ten Δ jest równy 16, zaś długości boków tego
Δ są kolejnymi liczbami parzystymi. Wyznacz najkrótszą wysokość tego trójkąta.
15 paź 21:12
irena_1:
1.
| | 4 | | 16 | | 9 | |
sin2α=1−( |
| )2=1− |
| = |
| |
| | 5 | | 25 | | 25 | |
a+b=c+2r
c=45cm
15 paź 21:23
Fasola022: Czy mogłabyś dodać do tego rysunek..?
15 paź 21:25
irena_1:
2.
P=pr
a=2n
b=2n+2
c=2n+4
(3n+3)*16=336
3n+3=21
3n=18
n=6
a=12
b=14
c=16
8h=336
h=42
15 paź 21:26
irena_1:
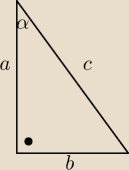
15 paź 21:28
Fasola022: czy sinα nie równa sie bc przy takim oznaczeniu na rysunku?
15 paź 21:43
Fasola022: przepraszam, coś mi się pomieszało− bramka mnie wytrąciła z równowagi chyba

15 paź 21:46
Eta:

2/ sposób
| | 4 | |
cosα=0,8 = |
| ⇒ b= 4k i c= 5k , k>0 |
| | 5 | |
a=
√25k2−16k2= 3k
2r
w= a+b−c ⇒ 3k+4k−5k=18 ⇒ k= 9
| | 1 | |
P= |
| *3k*4k= 6k2 = 6*81= 486 cm2 |
| | 2 | |
16 paź 01:10


 2/ sposób
2/ sposób