Zaznacz zbiór punktów spełniających równanie mAGDa: log_y+1 (x²−x) > log_x+1²(x²−x) . gdzie y∊ (−1, 0) Błagam o pomoc , wskazówki, cokolwiek

Mila: No masz źle przepisane zadanie ma być: log_y+1 (x²−x) > log_y+1²(x²−x) gdzie y∊ (−1, 0) D: x²−x>0⇔ x(x−1)>0⇔x<0 lub x>1 Dla y∊(−1,0) mamy −1<y<0 /+1 0<y+1<1 zatem funkcja logarytm jest malejąca log_y+1 (x²−x)*[1 −log_y+1(x²−x)] >0 log_y+1 (x²−x)=t t*(1−t)>0⇔ t>0 i t<1 log_y+1 (x²−x)>0 i log_y+1 (x²−x)<1 ⇔ log_y+1 (x²−x)>log_y+11 i log_y+1 (x²−x)<log_y+1(y+1)⇔ x²−x<1 i x²−x>y+1 x²−x−1<0 i y<x²−x−1i x∊D i y∊D Δ=5

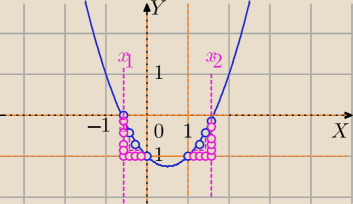
	1−√5		1+√5
x1=		lub x2=
	2		2

szukane obszary to trójkąty różowe