 Mam takie zadanie z funkcji kwadratowej którego nie potrafię zrobić:
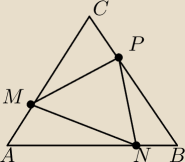
Trójkąt równoboczny ABC ma bok długości 20cm. Na jego bokach obrano punkty M,N,P tak, że
|AM| = |BN| = |CP| (jak na rysunku powyżej).
a) Oznacz długości odcinków AM, BN oraz CP literą x. napisz wzór funkcji pola trójkąta MNP w
zależności od długości x.
b) Jak należy wybrać punkty M,N i P, aby pole trójkąta MNP było najmniejsze?
Mam takie zadanie z funkcji kwadratowej którego nie potrafię zrobić:
Trójkąt równoboczny ABC ma bok długości 20cm. Na jego bokach obrano punkty M,N,P tak, że
|AM| = |BN| = |CP| (jak na rysunku powyżej).
a) Oznacz długości odcinków AM, BN oraz CP literą x. napisz wzór funkcji pola trójkąta MNP w
zależności od długości x.
b) Jak należy wybrać punkty M,N i P, aby pole trójkąta MNP było najmniejsze?
| 1 | ||
MN2 = x2 + 400 − 40x + x2 − 2(20x−x2)* | ||
| 2 |
| MN2√3 | ||
PMNP = | ||
| 4 |
| √3 | ||
f(x) = | *(3x2−60x+400) | |
| 4 |
| −b | 60 | |||
najmniejsze pole masz dla x = | = | = 10 | ||
| 2a | 6 |