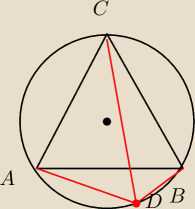
dowodzenie Buu: W okrąg wpisano trójkąt równoboczny ABC. Na okręgu wybrano punkt D (różny od punktów A, B, C) i poprowadzono trzy odcinki DA, DB, DC. Wykaż, że suma długości dwóch krótszych odcinków jest równa długości odcinka trzeciego.

Vax: Skorzystaj z twierdzenia Ptolemeusza.

Buu: nie znam, jest jakaś inna możliwość?

Buu: ...

Buu: proszę

Buu: ............

Buu: może jednak ktoś się skusi?

Buu: ....

Buu: ,,,,,,,,,,,,

amator: hmm, z pól nie wiem nadal jak zrobić (zadanie jest w dziale "zastosowanie pojecia pola w dowodzeniu twierdzen"), ale rzeczywiście twierdzeniem Ptolemeusza wychodzi genialnie łatwo tylko trzeba je najpierw znać Twierdzenie Ptolemeusza mówi (chyba jakoś tak) że jeżeli na czworokącie da się opisac okrąg to iloczyn przekątnych czworokąta jest równy sumie iloczynów boków leżacych naprzeciwko siebie, więc dla tego zadania |CD| * |AB| = |CB|* |AD| + |AC| * |DB| ale że AB = a , CB = a, AC = a ; "a" sie zredukują i koniec dowodu

amator: hmm, z pól nie wiem nadal jak zrobić (zadanie jest w dziale "zastosowanie pojecia pola w dowodzeniu twierdzen"), ale rzeczywiście twierdzeniem Ptolemeusza wychodzi genialnie łatwo tylko trzeba je najpierw znać Twierdzenie Ptolemeusza mówi (chyba jakoś tak) że jeżeli na czworokącie da się opisac okrąg to iloczyn przekątnych czworokąta jest równy sumie iloczynów boków leżacych naprzeciwko siebie, więc dla tego zadania |CD| * |AB| = |CB|* |AD| + |AC| * |DB| ale że AB = a , CB = a, AC = a ; "a" sie zredukują i koniec dowodu

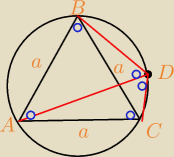
MrTomek795: Można to również rozwiązać korzystając z twierdzenia cosinusów. Niebieskie kropki 60 stopni. (kąty oparte na tym samym łuku) więc: a² = AD² + DC² − 2 AD x DC x cos60 a² = BD² + AD² − 2 AD x BD x cos60 / −1 jak dodamy 0 = DC² − BD² − AD x DC + AD x BD (cos 60 = 1/2) 0 = DC² − BD² + AD (BD − DC) (BD² − DC²) / (BD −DC) = AD AD = (BD − DC)(BD + DC) / (BD − DC) AD = BD + DC