Trygonometria Theemi: Hej. Witajcie ponownie. Tym razem piszę w związku z zadaniami z trygonometrii. Część mam, za jedno nie wiem jak się zabrać ale generalnie nie jest źle : ). Najpierw "wklikam" treść zadań. Chodzi mi generalnie o sprawdzenie i małe podpowiedzi. Zad 1. |3−4sinx|=a² + 3 Dla jakich a równanie jest sprzeczne ? Zad 2. Wyznacz zbiór wartości f(x)=1+2cosx−sin²x. Znajdź argument dla którego funkcja przyjmuje wartość najmniejszą. Zad 3. Wyznacz dziedzinę funkcji: ^{sinx(tgx+sinx)}_cosx(1+sinx). Uzasadnij że przyjmuje tylko wartości nieujemne. Jest jeszcze jedno za które nie wiem jak się zabrać ale spróbuję najpierw sam coś zdziałać : ). Zad 1. Obliczyłem zbiór wartości |3−4sinx|. Krok po kroku aż z sinx dotarłem do fazy końcowej. Wyszło <0,7>. To teraz a²+3<0 ? a²+3>7. Wyszło że a?(−∞,−2)?(−√3,√3)?(2,∞) Mam nadzieję że to zadanie dobrze zrobione : ). Zad 2. f(x)=1+2cosx−sin²x=1+2cosx−1+cos²x= cos²x+2cosx=t(t+2) jeżeli t=cosx t₁ =0 t₂ = −2 cosx≠−2 Obliczyłem jeszcze p =−1 (wierzchołek) Teraz f(−1) i f(0). Wychodzi odpowiednio −1,0 Ale jak znaleźć argument dla którego wartość przyjmuje wartość najmniejszą ? Zad 3. Wyznaczyłem dziedzinę. Czyli od R odjąłem to co wypada przez tangens, cosinus i mianownik. Ale jak zrobić drugi podpunkt w tym zadaniu ? Uzasadnij że przyjmuje tylko wartości nieujemne. Czyli mam uzasadnić że nie ma miejsc zerowych tak ? Jak to zrobić? Zad 4. Narysowałem wykres 1−|x−4|. Poniżej go umieszczę. Ale co dalej zrobić ?

Theemi: Brak treści do zadania 4.. Wyznacz liczbę dodatnich rozwiązań równania w zależności od m: 1−|x−4|=2sinm

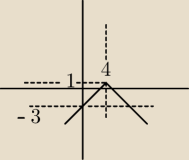
Theemi: wierzchołek w (4,1) a wykres dotyka OY w (0,−3)