zbiory
zadanie: udowodnij
a) (AUB)\(A∩B)=(A∩B')U(A'∩B)
15 paź 06:06
zadanie: ?
15 paź 13:02
Mila:
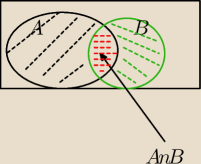
x∊(A∪B)\(A∩B)⇔x∊(A∪B)⋀x∉(A∩B)⇔x∊(A\B)⋁x∊(B\A)⇔
x∊(A∩B')U (B∩A')
15 paź 13:32
zadanie: tam na dole zamiast (B∩A') powinno byc chyba (A'∩B) ?
15 paź 13:37
Mila:
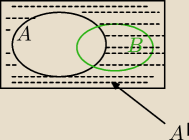
Może być i tak i tak. Tylko może jeszcze dokładniej trzeba rozpisac. Zobacz jak na ćwiczeniach
było.
15 paź 13:45
zadanie: nam raczej kazali udowadniac przez to, ze x nalezy niz przez diagramy
15 paź 13:46
zadanie: a mozna byloby to rozpisac jeszcze szerzej np ....... x∊(AUB).....⇔x∊A⋁x∊B ....... ?
15 paź 13:48
Mila:
Diagramy rysujemy, aby mieć lepszą orientację w problemie.
15 paź 13:49
Mila:
Tak, rozpisz .
15 paź 13:49
zadanie: to od poczatku
(AUB)\(A∩B)=(A∩B')U(A'∩B)
x∊(AUB)\(A∩B)⇔(x∊(AUB)⋀x∉(A∩B))⇔((x∊A ⋁ x∊B) ⋀ ¬(x∊ A∩B))⇔((x∊A ⋁ x∊B) ⋀¬(x∊A⋀x∊B))⇔dalej nie
wiem
15 paź 14:07
Mila:
⇔[x∊A⋀(x∊A'⋁x∊B')⋁x∊B⋀(x∊A'⋁x∊B')⇔
x∊A⋀x∊B' ⋁x∊B⋀x∊A'⇔x∊(A∩B')U(A'∩B)
15 paź 17:49
zadanie: dziekuje
16 paź 06:06
Mila:
Napisz, czy tak było na ćwiczeniach.
16 paź 15:43