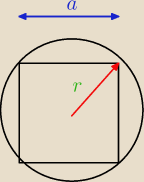
. asdf: Prawdopodobieństwo: Witam, Zad: w kolo wpisany jest kwadrat, wyznaczyc prawdopodobienstwo, ze punkt rzucony losowo na kolo znajdzie sie wewnątrz kdwadratu:

	m(A)
P(A) =		=
	m(Ω)

m(A) = a² m(Ω) = ...

	a√2
r =
	2

	a2π
m(Ω) =
	2

	2a2		2
P(A) =		=
	a2π		π

ok?

Trivial: OK.

asdf: Dzieki, nastepne: wewnatrz odcinka o dlugosci 1 obrano na "chybil trafil" dwa punkty, jakie jest prawdopodobienstwo, ze odleglosc miedzy tymi punktami jest mniejsza niz 1/3. Prosze o wskazowke

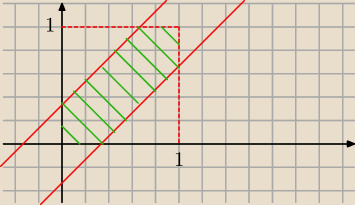
Trivial: Zmienne są niezależne.

	1		1		1
|y−x| <		→ y < x +		⋀ y > x −
	3		3		3

asdf: Dzięki, a to już z całki policzę

Trivial: asdf, z jakiej całki. o.o

	1		4		5
P = 1 − 2*		*(2/3)2 = 1 −		=		.
	2		9		9

asdf: chodziło mi o pole, całką też bym zrobił, tak samo:

	3   ( )2   10
1 − 2 *		= ..
	2

asdf: co ja pisze...chodzilo mi o to co Ty napisales, nie idzie sie skupic

Trivial: Masz jeszcze jakieś zadanko?

asdf: tak: Strzelec oddaje 3 strzaly do celu, Pb. trafienia za kazdym razem jest takie samo i wynosi

	2
		.
	3

a) wyznacyzsz rozklad i dystrybuante liczby trafien X. b) wyznaczyc rozklad zmiennych Y = 2X − 3 i Z = −Y² + 4 c) obliczyc wart. oczekiwaną i wariancje liczby trafien do tarczy d) korzystajac z odpowiednich wlasnosci wyznacyzc EY i D²Y, gdzie Y = −4X + 5 c i d − tego nie mialem, a)

	2		2		2
P(X=0) − 0 trafień: =		*		*
	3		3		3

	2		2		1		2		2		1		2
P(X =1) − 1 trafienie: =		*		*		+		*		*		+		*
	3		3		3		3		3		3		3

	2		1
		*
	3		3

	1		1		2
P(X=2) = 2 trafienia =		*		*		* 3
	3		3		3

	1
P(X=3) = 3 trafienia =
	33

b) w kolejnym poscie

asdf: b) Y = 2X −3 S_x = {0,1,2,3} S_y = {2*0−3, 2*1−3, 2*2−3, 2*3−3} teraz aby policzyć p_yi to muszę: P(Y = −3), P(Y = −1), P(Y=1), P(Y = 3) tak?

Trivial:

	3 0		1
P(X=0) =		*(1/3)3 =
			27

	3 1		6
P(X=1) =		*(1/3)2*(2/3) =
			27

	3 2		12
P(X=2) =		*(1/3)*(2/3)2 =
			27

	3 3		8
P(X=3) =		*(2/3)3 =
			27

asdf: schematu bernuliego nie mialem

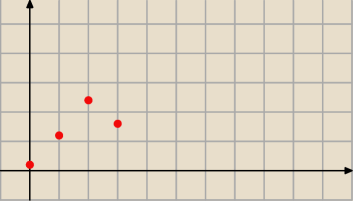
Trivial: Rozkład wygląda tak.

Trivial: asdf, ja nawet nie myślałem o schemacie Bernoulliego. Po prostu: P(X=k) = wybieramy k tarcz dla których było trafienie z 3 dostępnych. Prawdopodobieństwo

	2		1
trafienia jest		, prawdopodobieństwo nietrafienia jest		, zatem prawdopodobieństwo
	3		3

	3 k
uzyskania k trafień jest		*(2/3)k*(1/3)3−k.

asdf: Ok Dzięki Rozjaśnia się , to chodzi o wybranie, np. tego, ze trafie − T, N − nie trafienie. zbiór = {T,N,N}

	3 1
wybieramy 1 element z trzech (ze trafi), mozliwosci jest

tak to mam rozumieć?

Trivial: Ogólnie, wybierasz k tarcz w które zamierzasz trafić. Reszta to formalności.

Trivial: Btw, to rozkład dwumianowy jest. http://pl.wikipedia.org/wiki/Rozk%C5%82ad_dwumianowy

asdf: Rozumiem! Dzięki.

asdf: dla wyrzunia dwoch orlow w 5 rzutach to:

5 2		1		1
	* (		)3 * (		)2
		2		2

3 − jak sie nie uda 2 − jak sie uda

Trivial: Tak.

Trivial: Zrób podpunkt b).

Trivial: I jeszcze dystrybuanta w a).

asdf: ok − bylem obiad sobie zrobic

Trivial: Chyba śniadanie.

Eta: Ja też "objadałam"

bezendu: asdf już nie trzymasz kredensu ?

asdf: F(X) = e = ∊ {0 : x e (−inf;0>

	1
{		: x e (0;1>
	27

	1+6
{		: x e (1;2>
	27

	7+12
{		: x e (2;3>
	27

{1: x e (3;inf)

asdf: teraz trzymam widelec z krokietami, kredens nie upadnie...

bezendu: http://img2.demotywatoryfb.pl//uploads/201310/1381318392_g8nuog_600.jpg

asdf: Z = −Y² + 4: S_y = {−3,−1,1,3} S_z = {−5,3,3,−5} = {−5,3} P(Z = −5) =P(−Y² + 4 = −5) = P(Y=3) + P(Y =−3) = P(Y = 3) + 0 = P(Y=3) = ...tego nie policzylem w poprzednim wiec teraz nie mam wyniku ale to juz "drobnocha"

Trivial: asdf, zależy od definicji F(x). Ja wolę definiować F(x) jako F(x) = P(X ≤ x) Czyli

	⎧	0 x∊(−∞,0)
	⎜	1/27 x∊[0,1)
F(x) =	⎨	7/27 x∊[1,2)
	⎜	19/27 x∊[2,3)
	⎩	1 x∊[3,∞)

asdf: ja korzystam z F(x) = P(X < x)

asdf: http://i.qkme.me/3socr3.jpg dzisiejsza data: 15 pazdziernika

Trivial: Y = 2X − 3 Z = −Y² + 4 0 →^Y→ −3 →^Z→ −5 1 →^Y→ −1 →^Z→ 3 2 →^Y→ 1 →^Z→ 3 3 →^Y→ 3 →^Z→ −5

	9
P(Z = −5) = P(Y = −3) + P(Y = 3) = P(X = 0) + P(X = 3) =
	27

	18
P(Z = 3) = P(Y = −1) + P(Y = 1) = P(X = 1) + P(X = 2) =
	27

asdf: a no, troche sie przejechalem Dzieki za korekte, mam 101 zadan ze statystyki, podeslac Ci? Jedno z ciekawych zadan z wykladow: Jest odcinek a o dlugosci |a|, jakie jest prawdopodobienstwo, ze da sie z tego zbudowac trojkat?

Trivial: asdf, ja nie potrzebuje zadań ze statystyki. Statystyka to dla mnie stare dzieje.

Trivial: A tego zadania nie rozumiem. Jak można z jednego odcinka zbudować trójkąt?

asdf: spoko ale znalazlem tez 2 ciekawe, jak chcesz: Święty Mikołaj pakuje prezenty dla grzecznych i niegrzecznych studentów. Ma do zapakowania 7 identycznych lalek i 5 misiów, które różnią się kształtem ucha. Na saniach czekają już cztery różnokolorowe pudła. Na ile sposobów Święty Mikołaj może zapakować prezenty do pudełek (niektóre pudełka mogą być też puste – dla niegrzecznych studentów)? Na ile sposobów 12 szachistów może grać jednocześnie 6 partii?

asdf: Jest odcinek a o dlugosci |a|, dzielac go na 3 czesci, jakie jest prawdopodobienstwo, ze da sie z tego zbudowac trojkat ? *

Trivial: Poza tym jeszcze masz c) i d) do zrobienia! c) μ_X = E[X] = ∑_i=1..n p_i*x_i (średnia) d) Y = −4X + 5 E[Y] = E[−4X + 5] =^{liniowość E, E[c] = c} = −4μ_X + 5 D²[X] = E[(X−μ_X)²] = E[X² − 2μ_XX + μ_X²] = E[X²] − 2μ_XE[X] + μ_X² = E[X²] − 2μ_X² + μ_X² = E[X²] − μ_X² = E[X²] − (E[X])² Resztę pozostawiam Tobie.

asdf: c,d − nie mialem tego jeszcze na wykladach, musialbym doczytac, a liczyc w ciemno nie lubie (tzn. nie wiem co licze) − nie lubię

Trivial: wartość oczekiwana to po prostu średnia. wariancja to wariancja (było w szkole średniej...)

Trivial: A to zadanko z trójkątem jest "typowe".

asdf: wariancje w szkole bylo, ale wariacji bylo wiecej :−) i wariancje poszly na bok

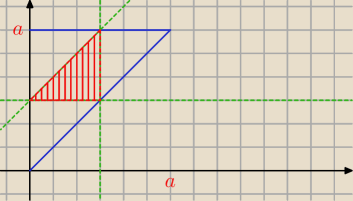
Trivial: Losujemy dwie liczby X,Y z przedziału [0, a]. Takie, że X < Y. Wylosowane liczby jednoznacznie określają podział odcinka na 3 części. Pierwsza z nich ma długość X Druga z nich ma długość Y−X Trzecia: a−Y Warunki są takie 1) X < Y−X + a−Y = a−X → 2X < a → X < a/2 2) Y−X < X + a−Y → 2Y < 2X + a → Y < X + a/2 3) a−Y < X + Y−X = Y → 2Y > a → Y > a/2

	1
P =		.
	4

asdf:

Trivial: Dobranoc, asdf.

asdf: Dobranoc Ja jeszcze mam troche do zrobienia