rozeta bartek: W kwadracie ABCD, o bkou długości 12 cm, zakreślono łuki okręgów a nastepnie pokolorowano wybrane jego cześci. Oblicz pole kolorowej figury na danym rysunku. http://img241.imageshack.us/img241/1334/10952672ed2.th.jpg

irena_1: Połowa tej figury to różnica między ćwiartką koła o promieniu 12cm i połowy kwadratu.

	1		1
PF=2*(		π*122−		*122)=2*(36π−72)=(72π−144)cm2
	4		2

tutu: P= 72(π−2) cm²

bartek: wyniki wychodzą inne 288−72π

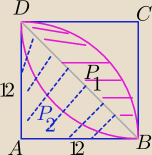
tutu: P(wycinka) = P₂(ΔABD) +P₁ P₁= P(wycinka − ćwiartki koła) − P(ΔABD −− połówka kwadratu))

	1		1		1		1
P1=		*π 122 −		*122 =122(		π−		)
	4		2		4		2

	1		1		1
P(łezki)= 2*P1= 144*2(		π−		) = 144*2*		( π −2)= 72(π−2) cm2
	4		2		4

irena_1: Tutu! Ale Twój wynik to nie jest pole "łezki", tylko tego, co zostaję z kwadratu po wycięciu "łezki'. sprawdź: 144−(72π−144)=288−72π

tutu: @ irena Nie bardzo wiem o co Ci chodzi? P₁ −−− pole połówki łezki P(łezki)= 2*P₁ P₁= ćwiartka pola koła − połówka pola kwadratu