W trójkąt równoboczny niekumaty: W trójkąt równoboczny ABC o boku 9 cm wpisano prostokąt PQRS w ten sposób, że wierzchołki P i Q należą do boku AB, wierzchołek R − do boku BC, S − do boku AC. Wyznacz długości boków prostokąta o maksymalnym polu.

AROB: pomagam

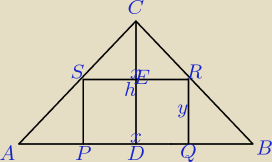
AROB: P = xy x,y − boki prostokąta, a − bok trójkąta równobocznego (przepraszam za trójkąt mało równoboczny)

	h		h − y		a√3		9√3
ΔCER∼ΔCDB ⇒		=		, h =		=
	a		x   2		2		2

9√3   2		9√3   −y 2
	=
9		x   2

	9√3		x		9√3
9(		− y) =		*		/:9
	2		2		2

9√3		x√3
	− y =
2		4

	9√3		x√3		18√3 − x√3		√3(18 − x)
y =		−		=		=
	2		4		4		4

Budujemy funkcję pola zależnego od boku x:

	√3(18 − x)		18√3x − √3x2		√3		9√3
P(x) = x *		=		= −		x2 +		x
	4		4		4		2

	−b		−9√3   2
Funkcja ta osiąga maksimum dla xW =		=		= 9
	2a		−2√3   4

	√3		9√3
y =		(18 − 9) =
	4		4

	9√3
Zatem boki prostokąta o maksymalnym polu są równe: x = 9, y =
	4

niekumaty: Dzięki

xxx: Witam. Moim zdaniem ta proporcja będzie wyglądała troszkę inaczej: z podobieństwa trójkątów ΔSRC~ΔABC mamy:

h		a   2
	=
h−y		x   2

	9√3		x√3
y=		−
	2		2

	9√3		x√3
P(x)=xy=x(		−		)
	2		2

	b
xmax=−
	2a

Wtedy

	9√3
x=4,5, a y=
	4

Pozdrawiam.