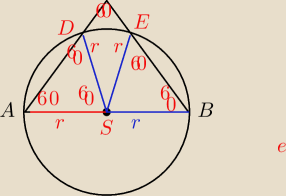
 Podstawa trójkąta równobocznego jest średnicą koła o promieniu r. Oblicz stosunek pola części
koła leżącej na zewnątrz trójkąta do pola części koła leżącej wewnątrz tego trójkąta.
|∢CAB|=60° i |∢CBA|=60°
Trójkąty ASD i BSE są równoramienne.
Stąd: |∢ADS|=60° i |∢BES|=60°
I: |∢DSA|=60°, |∢ESB|=60°
Zatem trójkąty ASD i BSE są równoboczne.
P(ΔASD)=P(ΔBSE)=r²√3/4
|∢DSE|=60°
Pw=60°/360°·πr²=¹/₆πr²
P(części wewn. △)=r²√3/4+r²√3/4+¹/₆πr²=r²√3/2+¹/₆πr²
P(części na zewn. △)=πr²−(r²√3/2+¹/₆πr²)=⁵/₆πr²−r²√3/2
P(części na zewn. △)/P(części wewn. △)=(⁵/₆πr²−r²√3/2)/(r²√3/2+¹/₆πr²)=
r2(5π − 3√3) 6
−−−−−−−−−−−−−−−−−−−− * −−−−−−−−−−−−
6 r2(3√3 + π)
po skróceniu: 5π − 3√3
−−−−−−−−−−−
π +3√3
według odpowiedzi jest to: 2π − 3√3
−−−−−−−−−−−−−−
π +3√3
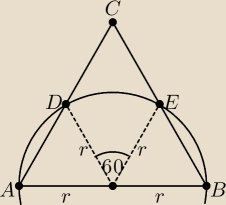
Podstawa trójkąta równobocznego jest średnicą koła o promieniu r. Oblicz stosunek pola części
koła leżącej na zewnątrz trójkąta do pola części koła leżącej wewnątrz tego trójkąta.
|∢CAB|=60° i |∢CBA|=60°
Trójkąty ASD i BSE są równoramienne.
Stąd: |∢ADS|=60° i |∢BES|=60°
I: |∢DSA|=60°, |∢ESB|=60°
Zatem trójkąty ASD i BSE są równoboczne.
P(ΔASD)=P(ΔBSE)=r²√3/4
|∢DSE|=60°
Pw=60°/360°·πr²=¹/₆πr²
P(części wewn. △)=r²√3/4+r²√3/4+¹/₆πr²=r²√3/2+¹/₆πr²
P(części na zewn. △)=πr²−(r²√3/2+¹/₆πr²)=⁵/₆πr²−r²√3/2
P(części na zewn. △)/P(części wewn. △)=(⁵/₆πr²−r²√3/2)/(r²√3/2+¹/₆πr²)=
r2(5π − 3√3) 6
−−−−−−−−−−−−−−−−−−−− * −−−−−−−−−−−−
6 r2(3√3 + π)
po skróceniu: 5π − 3√3
−−−−−−−−−−−
π +3√3
według odpowiedzi jest to: 2π − 3√3
−−−−−−−−−−−−−−
π +3√3

| 1 | 1 | |||
Pole części koła wewnątrz trójkąta: Pw = 2* | r2√3 + | πr2 | ||
| 4 | 6 |
| 5 | 1 | |||
Pole części kola na zewnątrz trójkąta: Pz = πr2 − Pw = | πr2 − | r2√3 | ||
| 6 | 2 |
| Pz |
| 6 | ||||||||||||||||||
= | * | = | ||||||||||||||||||
| Pw |
| 6 |
| 5π − 3√3 | ||
= | ||
| 3√3 + π |
| 1 | ||
czyli Pz = | πr2 − Pw | |
| 2 |
