zadanie z ostrosłupów
sony1540: 1. W ostrosłupie prawidłowym trójkątnym kąt nachylenia ściany bocznej do płaszczyzny
podstawy wynosi 60o. Krawędź podstawy ma długość 6cm. Oblicz objętość i pole
powierzchni całkowitej bryły.
14 paź 12:08
Janek191:
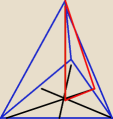
α = 60
o
a = 6 cm
Mamy
h
1 − wysokość trójkąta równobocznego
h
1 = a
√3[2} = 6
√3{2} cm = 3
√3 cm
| | 1 | | 1 | |
x = |
| h1 = |
| * 3 √3 cm = √3 cm |
| | 3 | | 3 | |
h − wysokość ostrosłupa
h
2 − wysokość ściany bocznej ( Δ równoramienny )
więc
| h | |
| = tg 60o = √3 / * √3 |
| √3 | |
h = 3
oraz
czyli
h = 3 cm
−−−−−−−
h
2 = 2
√3 cm
−−−−−−−−−−
Objętość ostrosłupa
| | 1 | | 1 | | √3 | | 1 | | √3 | |
V = |
| Pp * h = |
| *a2 |
| * h = |
| *62 * |
| * 3 = 9 √3 |
| | 3 | | 3 | | 4 | | 3 | | 4 | |
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Pole powierzchni całkowitej
| | √3 | | √3 | |
Pc = Pp + Pb = a2 |
| + 3*0,5 a*h2 = 62 |
| + 1,5*6*2√3 = |
| | 4 | | 4 | |
= 9
√3 + 18
√3 = 27
√3
−−−−−−−−−−−−−−−−−
Odp. V = 9
√3 cm
3, P
p = 27
√3 cm
2
==================================
14 paź 12:45
Janek191:

α = 60
o
a = 6 cm
Mamy
h
1 − wysokość trójkąta równobocznego
h
1 = a
√3[2} = 6
√3{2} cm = 3
√3 cm
| | 1 | | 1 | |
x = |
| h1 = |
| * 3 √3 cm = √3 cm |
| | 3 | | 3 | |
h − wysokość ostrosłupa
h
2 − wysokość ściany bocznej ( Δ równoramienny )
więc
| h | |
| = tg 60o = √3 / * √3 |
| √3 | |
h = 3
oraz
czyli
h = 3 cm
−−−−−−−
h
2 = 2
√3 cm
−−−−−−−−−−
Objętość ostrosłupa
| | 1 | | 1 | | √3 | | 1 | | √3 | |
V = |
| Pp * h = |
| *a2 |
| * h = |
| *62 * |
| * 3 = 9 √3 |
| | 3 | | 3 | | 4 | | 3 | | 4 | |
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Pole powierzchni całkowitej
| | √3 | | √3 | |
Pc = Pp + Pb = a2 |
| + 3*0,5 a*h2 = 62 |
| + 1,5*6*2√3 = |
| | 4 | | 4 | |
= 9
√3 + 18
√3 = 27
√3
−−−−−−−−−−−−−−−−−
Odp. V = 9
√3 cm
3, P
p = 27
√3 cm
2
==================================
14 paź 12:46
sony1540: Dzieki kolego a dałbyś radę zrobić jeszcze inne zadania które wrzuciłem ? Byłbym bardzo
wdzieczny za pomoc ?
14 paź 12:58
 α = 60o
a = 6 cm
Mamy
h1 − wysokość trójkąta równobocznego
h1 = a√3[2} = 6 √3{2} cm = 3√3 cm
α = 60o
a = 6 cm
Mamy
h1 − wysokość trójkąta równobocznego
h1 = a√3[2} = 6 √3{2} cm = 3√3 cm
 α = 60o
a = 6 cm
Mamy
h1 − wysokość trójkąta równobocznego
h1 = a√3[2} = 6 √3{2} cm = 3√3 cm
α = 60o
a = 6 cm
Mamy
h1 − wysokość trójkąta równobocznego
h1 = a√3[2} = 6 √3{2} cm = 3√3 cm