Równanie trygonometria sinx+1 = tgx Micodin: Rozwiąż równanie sinx + 1= tgx dla x∊(−^π₂, ^π₂).

irena_1: Według mnie to równanie nie ma rozwiązań.

	π
W przedziale (−		; 0>
	2

− wartości L=(sinx+1) przebiegają wartości zbioru (0; 1> − wartości P=tgx przebiegają wartości przedziału (−1; 0>

	π
W przedziale (0;		)
	2

− wartości L=(sinx+1) przebiegają wartości przedziału (1; 2) − wartości P=tgx przebiegają wartości przedziału (0; 1)

	π		π
W przedziale (−		;		) nigdy lewa strona nie będzie równa prawej
	2		2

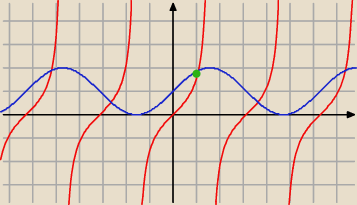
Aga1.: Rozwiązanie graficzne i widać,że jest jedno rozwiązanie w podanym przedziale.