skala trójkątów
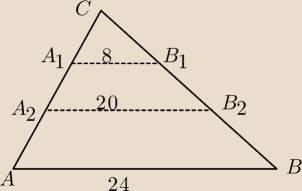
keti: Podstawa AB trójkąta ABC ma długość 24cm. Na boku AC zaznaczono punkty A1, A2, a na boku BC
punkty B1, B2 w taki sposób, że A1B1 II AB i A2B2 II AB. Wiedząc, że A1B1=8cm, A2B2=20CM,
oblicz stosunek pól:
a) trójkątów A1B1C, A2B2C i ABC
b) figur A1B1C, A2B2C, ABB2A2.
13 paź 20:12
Mila:
Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa.
1) A
1B
1|| AB⇒
| | 8 | | 1 | |
ΔA1B1C∼ΔABC w skali k1= |
| = |
| |
| | 24 | | 3 | |
| PΔA1B1C | | 1 | | 1 | |
| = ( |
| )2= |
| =1:9 |
| PΔABC | | 3 | | 9 | |
2)A
2B
2|| AB⇒
| | 20 | | 5 | |
ΔA2B2C∼ΔABC w skali k1= |
| = |
| |
| | 24 | | 6 | |
| PΔA2B2C | | 5 | | 25 | |
| =( |
| )= |
| = 25:36 |
| PΔABC | | 6 | | 36 | |
Dalej poradzisz sobie?
13 paź 22:18