Planimetria xyz: Kilka zadań z planimetrii, których nie mogę zrobić, proszę o pomoc

	AP
1. W trójkącie ABC dwusieczna kąta ACB przecina bok AB w punkcie P. Wykaż, że		=
	AC

	BP
	BC

2. Dany jest trójkąt prostokątny równoramienny ABC o przeciwprostokątnej rownej 2. Niech punkt P będzie takim punktem tego trójkata, że suma jego odległości od wierzchołków trójkąta jest najmniejsza. Wykaż, że suma ta jest równa 1 + √3

KUZDE: z tw. sinusow 1

Mila: 2) Jeżeli punkt P został tak wybrany, że suma jego odległości od wierzchołków trójkąta jest najmniejsza, to każdy z trzech kątów przylegających do P ma miarę 120^o. P− punkt Torricellego.

Mila: 2) Przeczytaj o punkcie Torricellego. Rozwiąż np. tak. P_ΔABC=1 1) porównaj sumę pól małych Δ z polem ΔABC⇒obliczysz sumę (xy+xz+yz) 2) W każdym "małym" Δ zastosuj twierdzenie cosinusów⇒otrzymasz układ równań. 3)Rozwiąż układ równań.

xyz: a czy można te zadania zrobić bez twierdzenia sinusów i cosinusów?

Mila: Nie miałeś tych wzorów?

xyz: nie, nie miałam, przerobiliśmy trygonometrię, ale bez twierdzeń sinusów i cosinusów.

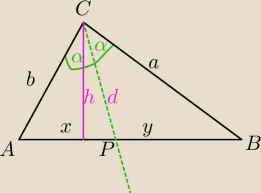
Mila: Dobrze, to pomyślę nad inna wskazówką. W której jesteś klasie? 1) Twierdzenie o dwusiecznej kąta w trójkacie: Z. CP^→ dwusieczna kąta ACB

	AP		BC
T.		=
	AC		BP

	1
PΔAPC=		x*h
	2

	1
PΔCPB=		*y*h
	2

	1		1		b*d*sinα
PΔAPC=		*b*d*sinα=		x*h⇔b*d*sinα=x*h⇔h=
	2		2		x

	1		1		a*d*sinα
PΔCPB=		*a*d*sinα=		*y*h⇔a*d*sinα=y*h⇔h=		⇔
	2		2		y

b*d*sinα		a*d*sinα
	=		⇔
x		y

b		a
	=
x		y

cnw

xyz: klasa 1, rozumiem ten sposób rozwiązania, dziękuję bardzo! A zadanie 2?

Mila: Później.

xyz: Okok

Mila: 2) a) narysuj trójkąt, zaznacz P. b) Na przeciwprostokątnej będziesz miała "oparty" równoramienny ΔABP o kącie 120² w wierzchołku P. Oblicz wysokość . c) Oblicz pole na dwa sposoby. d) oblicz jakie zostało pole. dalej sobie poradzisz.