granica Alois~: mam już rozwiązane ale nie rozumiem fragmentów 1) f(x)= e^−x sinx + x Df =R

	f(x)		e−x sinx + x
m= limx→∞ =		=limx→∞
	x		x

	sinx
= limx→∞ (e−x		+1 )
	x

chodzi o to że skąd mam tam 0 ? i tak samo tutaj n=lim_x→∞ [f(x) − mx] = lim_x→∞ {e^−xsinx + x − x ] = =lim_x→∞ e^−xsinx = 0 i to że też skąd wiem że 0 wiem głupie pytania pewnie :<

ICSP: 0 * 0 = 0 − to nie jest żaden symbol nieoznaczony

eR:

	e−x		sinx		x
limx→∞[		*		+		] =
	x		x		x

	1		sinx		x
= limx→∞[		*		] + limx→∞		=
	x*ex		x		x

= 0 + 1

Alois~: hmm moze inaczej jak będe mieć lim _x→∞ e^−x to jest to równe 0 tak ? lim _x→∞ e^−4x też 0 ?

	cosx
albo lim x→∞		tez 0 ? analogicznie do poprzednich przykladow
	x

eR: 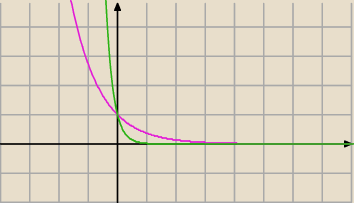f(x) = e^−x

	1
limx→∞[e−x] = limx→∞[		] = 0
	ex

g(x) = e^−4x

	1
limx→∞[e−4x] = limx→∞[		] = 0
	e4x

eR:

	cosx
lim		mozna obliczyc za pomoca twierdzenia o trzech funkcjach.
	x

eR: Liczbe "e" chyba znasz?

Alois~: poznałam kilka dni temu

Alois~: a i dzięki eR