Funkcja kwadratowa elongacja: Prosze o wmiarę etapowe rozwiązanie. Dana jest funkcja f(x)=a(x−7)(x+1) której najmniejsza wartość jest równa −4. Wyznacz współczynnik a.

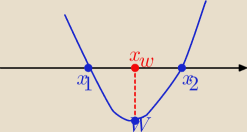
eR: f(x) = a(x²−6x−7) = ax² −6ax−6a, wiec bedzie to funkcja kwadratowa, ktorej wykres to parabola. Aby mial najmniejsza wartosc, to ramiona musza byc skierowane do gory, a wierzcholek powinien byc w punkcie (x, −4).

Kaja: skoro najmniejsza wartość to −4, to znaczy że wykres funkcji kwadratowej ma ramiona skierowane w górę, a ta wartość −4 jest przyjmowana w wierzchołku. policzmy zatem współrzędną x

	7+(−1)
wierzchołka: xw=		=3 (to 7 i −1 to miejsca zerowe)
	2

wtedy: −4=a(3−7)(3+1) −4=−16a

	1
a=
	4

elongacja: dlaczego dzielone przez 2 skoro we wzorze jest dzielone przez 2a a my nie wiemy ile ma a?

sara:

	x1+x2
xw=
	2