Planimetria - wen okrag trocina: Witam. Mam problem z zadaniem, kompletnie go nie rozumiem. Mogłby ktoś rozwiązać ? Z Góry dziękuje na kwadracie opisano okrag i wpisano wen okrag. pole powstalego pierscienia kolowego jest rowne 4 pi. oblicz pole kwadratu

Aga1.:

	a√2
R=
	2

	1
r=		a
	2

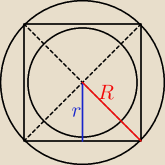
Pole pierścienia=Pole dużego koła − pole małego koła πR²−πr²=4π R²−r²=4 Podstaw za R i r i oblicz a.

PW: Niech kwadrat ma bok o długości a Okrąg opisany ma promień równy połowie przekątnej kwadratu, czyli ... (przekątną z twierdzenia Pitagorasa).

	a
Okrąg wpisany ma promień równy		.
	2

Warto zrobić rysunek. Pola tych dwóch kół obliczymy bez trudu, ich różnicę też, a ma być ona równa 4π. Myślę, że w całym zadaniu (rozwiązaniu) najtrudniejsze jest pierwsze zdanie.

PW: O, licho! Chciałem podpowiedzieć, a tu gotowe rozwiązanie.

Aga1.: Witaj PW. Nie ma gotowca, musi się jeszcze trochę potrudzić.

PW: Ciekawe, czy da radę. Napisz, trocino.

trocina: ¹₄= 4 ? i co dalej ?

PW: Zgubiłeś a (liczby R i r są zależne od a, Aga1 wyliczyła je nawet i napisała co zrobić).

trocina: (^a√2₂)² − (¹₂a)² = 4 ^2a2₄ − ¹₄a² = 4 i nie wiem jak to ogarnac

Antek:

	1		4
=		a2=4 to a2=		=4*4=16 to a=√16= ile lub a=−√16= ile .
	4		1   4

Ale bok nie moze miec wartosci ujemnej wiec zostale tylko ile ?

PW: Oj, trocina, skup się, bo zaczniemy tłumaczyć na krowach. Miałeś dwie ćwiartki krowy odjąć jedną ćwiartkę krowy i nie wiedziałeś co zrobic? Tylko nie tłumacz, że miałeś wątpliwości, czy ćwiartki były tylne, czy przednie.