pole obszaru -całka ankisiak1990: obliczyć pole obszaru D określonego nierównościami x²+y²≥1 (y−1)²+x²≤1, y≥√3x jak to rozwiązać ktoś może pomóc albo podpowiedzieć jak zacząć? z góry dziękuję

Mila: 1) rysunek 2) współrzędne biegunowe.

Mila: https://matematykaszkolna.pl/forum/213941.html

ankisiak1990: czyli moje granice będą takie r∊(0,1)

	π
α∊(0,		)
	3

czyli

	π
∫10dr∫π30r dα=
	6

Mila: x=r cosα y=r sinα x²+y²≥1⇔r²cos²α+r²sin²α≥1⇔r²≥1⇔r≥1 i y²−2y+1+x²≤1 r²sin²α−2rsinα+r²cos²α≤0 r²−2rsinα≤0⇔r(r−2sinα)≤0, r>0 i r≤2sinα Czyli r≥1 i r≤2sinα

	π		2π
α∊<		,		>
	3		3

ankisiak1990: ok promień rozumiem dlaczego taki, ale mam problem cały czas z wyznaczaniem kąta mogłabyś mi wytłumaczyć jak wylicza się kąt Z góry dzięki

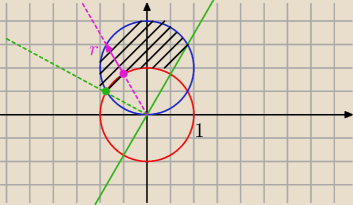
Trivial: Wyznaczmy granice na r. Z równania niebieskiego okręgu mamy: (y−1)² + x² = 1 y² + x² − 2y = 0 r² − 2rsinφ = 0 r = 2sinφ Zatem 1 ≤ r ≤ 2sinφ Wyznaczamy granice na φ:

	π
Z prawej strony mamy prostą y = √3x, zatem tanφ = √3 → φ =		.
	3

Z lewej strony mamy przecięcie okręgów. Zatem:

	1		5π
2sinφ = 1 ⇔ sinφ =		→ φ =
	2		6

	π		5π
Zatem		≤ φ ≤
	3		6

Pozostało obliczyć objętość:

	2√3+π
V = ∬V dV = ∫π/35π/6 dφ ∫12sinφ rdr =		≈ 1.65142
	4

Mila: A!, rzeczywiście, tak to jest, gdy się nie patrzy uważnie na rysunek. To pięknie dziękuję, zawsze trzeba dążyć do prawdy.

Mila: Idę zrobić deser, może poprawi mi się spostrzegawczość.

Trivial: Smacznego. (: