Problem Piotr 10: Dla jakich k okrąg o równaniu x²+y²−6x−2ky+2k²−10k+9=0 zawiera się w zbiorze A={(x;y): x≥0 ⋀ y≥0}. (x−3)²+(y−k)²=10k−k² S(3;k) ⋀ 10k−k² >0 k≥0 ⋀ k∊(0;10) Hmm? Co jeszcze trzeba uwzględnić?

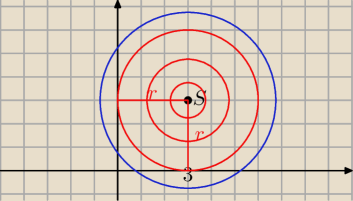
Basia: ten okrąg musi się "zmieścić" w I ćwiartce układu współrzędnych (czyli w A) może być taki jak te czerwone, ale już nie taki jak ten niebieski 1. r=10k−k²≤3 2: x_s−r = k−10k+k² = k²−9k ≥ 0

Piotr 10: Zamiast x_s powinno być y_s , tak? w Drugim punkcie

Basia: tak oczywiście; y_s

Piotr 10: A i jeszcze r=√10k−k² , czyli y_s − √10k−k² ≥0?

Basia: czyli √10k−k² ≤ 3 i k − √10k−k² ≥ 0 nie wiem dlaczego wydawało mi się, że już piszesz o r, a nie o r²

Piotr 10: Ta drugą nierowność to tak k≥√10k−k² Można podnieść do kwadratu gdyż k≥0, tak?

Basia: plus oczywiście te dwa warunki, które sam na początku podałeś k≥0 i k∊(0;10) czyli ostatecznie: 1. k∊(0;10) 2. √10k−k² ≤3 3. k − √10k−k² ≥ 0

Piotr 10: Ok. Dziękuję za pomoc . Dobranoc

Basia: jak najbardziej, ewentualnie odrzucisz tzw.rozwiązanie obce (czyli ujemne) gdyby się pokazały