analiza PuRXUTM:

	π
Pokaż że arctg x + arcctgx=
	2

Mila:

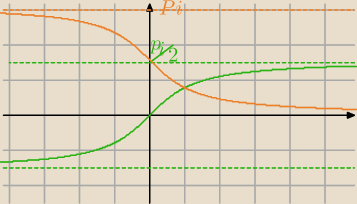
	π		π
y=arctg(x), x∊R, y∊(−		,		)
	2		2

y=arcctg(x), x∊R, y∊(0,π)

	π
arcctg(x)=		−arctg(x)
	2

	π		π
arctg(x)+		−arctg(x)=
	2		2

PuRXUTM: dziękuje, ale to chyba trzeba jakoś algebraicznie wykazać, ten ćwiczeniowiec mnie rozwalił, jak można tyle nowych zadań zadać...

Basia: y₁ = arctgx ⇔ tgy₁ = x y₂ = arcctgx ⇔ ctgy₂ = x y₁ ∊ (−^π₂;^π₂) y₂ ∊ (0;π) stąd: y₁+y₂ ∊ (−^π₂; ^3π₂) x = ctgy₂ = tg(^π₂−y₂) tgy₁ = tg(^π₂−y₂) y₁ = ^π₂−y₂+kπ y₁+y₂ = ^π₂+kπ czyli y₁+y₂ = ^π₂ bo dla każdego k≠0 ^π₂+kπ∉(−^π₂; ^3π₂)