trójkąt wpisany w okrąg
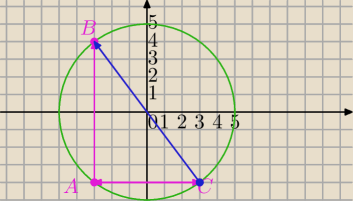
helpo: Trójkąt ABC jest wpisany w okrąg o równaniu x2 + y2=25. Wyznacz wierzchołki tego trójkąta,
jeśli
a) AB = [0,8] oraz CB = [−6, 8]
10 paź 19:39
helpo: Naprawdę nikt tego nie potrafi?
10 paź 19:46
Mila:
x
2+y
2=5
2
A,B,C∊okręgu⇔
współrzędne punktów spełniają równanie okręgu
i
AB = [0,8]
A=(a
1,a
2),B=(b
1,b
2)
b
1−a
1=0 i b
2−a
2=8
a
1=b
1, b
2=a
2+8
(*) a
12+a
22=25
a
12+(a
2+8)
2=25⇔a
12+a
22+16a
2+64=25⇔
25+16a
2+64=25
16a2=−64
a
2=−4 , b
2=−4+8
A=(−3,−4)
B=(−3,−4+8)=(−3,4)
oraz CB = [−6, 8]
⇔b1−c1=−6 i b2−c2=8
b1=c1−6 i b2=c2+8⇔
−3=c1−6 i 4=c2+8
c1=3 i c2=−4
C=(3,4)
10 paź 21:52
Mila: C=(3,−4)
10 paź 21:53