zad Matma: zbuduj kat o mierze α,α∊9o,90)takiej ze cosα=1/2√2 tgα=√7

Matma: wyznacz pozostale wartosci tryg. kata α

Matma: poslugujac sie wzorem cos2α=1−2sin²α oblicz sin15

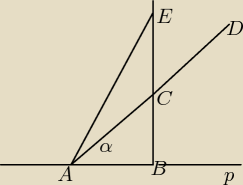
AS: 1. Na prostej p odłożyć odcinek AB = 1 2. W punkcie B wystawić prostopadłą BC = AB = 1 3. Na mocy tw.Pitagorasa AC = √2 4. Przedłużyć odcinek AC i odłożyć CD = AC − wtedy AD = 2*√2 5. Promieniem AD zakreślić łuk przecinający półprostą BC w punkcie E 6. Odcinek AE = AD = 2*√2

	AB		1
7. cos(α) =		=
	AE		2*√2

Matma: o dzikei AS

Matma: mam jeszcze pare

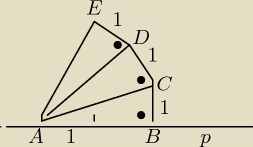AS: 1. Na prostej p odkładamy odcinek = 2*1j 2. W punkcie B wystawiamy odcinek BC = 1 3. Wtedy AC = √5 (= √2² + 1²) 4. W punkcie C wystawiamy odcinek CD = 1 prostopadły do AC 5. AD = √6 6. W punkcie D wystawiamy odcinek DE = 1 prostopadły do AD 7. AE = √7 8. Na prostej odłożyć odcinek MN = 1 9. W punkcie N wystawić prostopadłą NP = AE

	NP
10 W trójkącie MNP tg(α) =		= √7
	MN

AS: Uzupełnienie w punkcie 1 − odcinek AB = 2*1j w punkcie 2 − odcinek BC = 1 prostopadły do AB