kula Izka: Dwie przystające kule o promieniu długości R są tak położone że środek jednej z kuli lezy na powierzchni drugiej. Oblicz długość linii przecięcia powierzchni tych kul. Prosze o dokładny rysunek i co i jak, bo próbowałem i mi wychodza głupoty, ze niby ta część to R

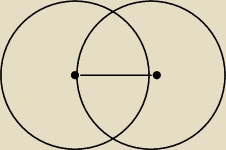
Matma: ja bym tez powiedziala ze to R

Matma: troche dupnie mi ten rysunek wyszedl ale ja bym to tak zrobila

Izka: ale to jest źle bo w odp jest inny wynik

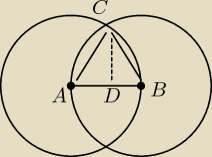
AS: AB = R ΔABC równoboczny (AB = BC = AC = R)

	R*√3
CD jest wysokością trójkąta równobocznego: CD =
	2

Częścią wspólną jest okrąg o promieniu CD Długość tego okręgu

	R*√3
M = 2*π*CD = 2*π*		= π*R*√3
	2