Znajdź długości przekątnych równoległoboku
Konkordia: Pole równoległoboku o bokach równych 5 i 7 wynosi 21. Znajdź długości przekątnych tego
równoległoboku. Proszę o pomoc! Nie mam pomysłu jak rozwiązać to zadanie.
10 paź 18:26
Asia: nie było podanego kąta pomiędzy a i b ?
wtedy to byłoby proste
11 paź 14:39
ICSP: kąt jest podany

P = absinα gdzie α jest katem miedzy bokami a oraz b
11 paź 14:44
Asia: a = 7, b = 5
P = ah
h=P/a = 3
x2 + 32 = 52
x2 = 4
cosα = 4/5
d1 = √a2 + 2abcosα + b2 = √49 + 56 + 25
d2 = √a2 − 2abcosα + b2 = √49 − 56 + 25
11 paź 14:54
Mila:
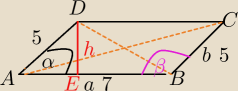
a*h=21
7*h=21
h=3
|AE|=4 Δ egipski (AE
2=5
2−3
2=16)
α+β=180
β=180−α
| | −4 | |
cosβ=cos(180−α)=−cosα= |
| |
| | 5 | |
|AC|=
√130
|DB|
2=18
|DB|=
√18=3
√2
11 paź 15:24
 P = absinα gdzie α jest katem miedzy bokami a oraz b
P = absinα gdzie α jest katem miedzy bokami a oraz b
 a*h=21
7*h=21
h=3
|AE|=4 Δ egipski (AE2=52−32=16)
a*h=21
7*h=21
h=3
|AE|=4 Δ egipski (AE2=52−32=16)