analiza matematyczna PuRXUTM: Policzyć arc tg 1, arc tg 0,arc tg (−1), arcsin(1/2), arccos(−1/2) od razu mówię że nigdy tego nie liczyłem i nie mam pojęcia jak to zrobić

Trivial: To zadanie jest bardzo proste. Skorzystaj z definicji arctgx (chodzi o zbiór wartości) i wyznacz taką liczbę y, że x = tg(y). Analogicznie dla arcsin, arccos.

PuRXUTM: arc tgx=y gdy tgy=x czyli dla arc tg 1 x=1

	π
czyli tgy=1 y=		+kπ
	4

Trivial: Tak, to rozwiązanie ogólne. Teraz proszę wyszukać rozwiązanie ze zbioru wartości arctg(x).

PuRXUTM:

	π		π
Zw=(−		;		) tak ?
	2		2

	π
y=
	4

Trivial: Tak.

PuRXUTM: arc tg 0=0

PuRXUTM:

	π
arc tg (−1)=−
	4

Trivial: OK.

PuRXUTM:

	π
arc sin 0.5=
	6

Trivial: Dobrze, teraz najtrudniejszy przykład z arccos.

PuRXUTM:

	2π
arccos(−0,5)=
	3

asdf: http://www.etrapez.pl/blog/funkcje-cyklometryczne-wyklad-video/ @Trivial Masz moze chwile na programowanie? Chodzi mi o klasy.

Trivial: asdf mam ale nie teraz. Za jakąś godzinkę.

Trivial: PuRXUTM, wszystko dobrze.

asdf: @Trivial Ok, to o 19:30 wrzucę temat na forum

Trivial: Możesz wrzucić teraz. Jak przyjdę to zerknę.

asdf: Dopiero z uczelni wrocilem, a skoro nie mozesz teraz to chcialem sie chwile przespac, podesle linka ok (od 8 do 18 na uczelni, moj mozg nie chce myslec)

asdf: podesle linka po 19*

Trivial: k

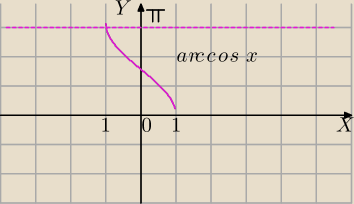
Mila: y=arccos(x) wykres arccos(−x)=π−arccos(x)

	1		1		π		2π
arccos(−		)=π−arccos(		)=π−		=
	2		2		3		3

	1		1		1
arccos		=α⇔cos(arccos(		))=cosα⇔cosα=
	2		2		2

	π
α=
	3

Mila:

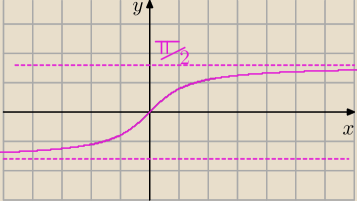
	π		π
y=arctg(x), y∊(−		,		)
	2		2

[Narctg(−x)=−arctg(x)]] ! funkcja nieparzysta

	π
arctg(−√3)=−arctg(√3)=−
	3

PuRXUTM: dzięki wielkie

Mila: Coś jeszcze z tego materiału?