wyjasnienie do rozwiazania - wartosc bezwzgledna Agataku: Dla x ∊ (1,2) zapisz wyrażenie |2x−5|+4|1−2x|,nie używając symbolu wartości bezwzględnej. Rozwiązanie: [mam w ksiązce ale musze wiedziec jak samemu rozwiazywac tego typu zadania, mam wiecej do rozwiazania] 1.

	⎧	2x−5 dla x∊ <52;+∞)
|2x−5|	⎩	−2x+5 dla x∊(−∞,52)

	⎧	1−2x dla x∊ (−∞,12>
|1−2x|	⎩	−1+2x dla x∊(12;+∞)

nie jestem pewna jak ustalić przedzial nalezacy do x , chodzi o to by wyliczyc x przyrownujac do zera owe liczby w wartosci bezwzglednej? 2x−5=0 |:2 1−2x=0|:2 x−5/2=0 x=1/2 x=5/2 skad wiem ze np w 2x−5 jest dla x∊ <⁵₂;+∞) a nie (−∞;⁵₂) itp? jesli ktos potrafilby do tego momentu wyjasnic mi w jaki sposob to jest wykonane to bylabym wdzieczna , bo dalsza czesc rozwiazania jest jasna dla mnie,

Asia.: Po pierwsze, ponieważ masz w module zapis 2x−5, może mieć od dwie wartości : 2x−5 lub −2x+5, a to dlatego, że wyjmując z modułu (czy jak to się tam mówi) jakąś liczbę może być ona dodatnia lub ujemna. Jeżeli jest ona bez zmian (2x−5) należy do przedziału od x (dowolnej liczby, w Twoim przypadku jest to ułamek) do +∞. Jeżeli jest ona zmieniana na minus (−2x+5) należy do przedziału od −∞. A następnie przyrównujesz obie wartości do zera Mam nadzieję, że pomogłam

Agataku: jezeli jest bez zmian to łącznie z tą liczbą , czyli nawiasy "<" albo ">" przy tej liczbie zawsze? bynajmniej mam tak w tym przykladzie, z tego co widze w tym rozwiazaniu jednak to drugie |1−2x| jest odwrotnie do tego co mowisz tzn nie zmieniajac znaku mam od −∞ do x, dopiero po zmienieniu znakow mam od x do +∞ chodzi tu o kolejnosc tych "modulow" w jednym jest tak, a w drugim odwrotnie i tak jest zawsze czy o co tu chodzi, od czego to zalezy?

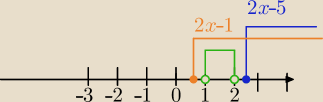
Mila: f(x)=|2x−5|+4|1−2x| dla x∊(1,2)

	5
|2x−5|=2x−5 dla 2x−5≥⇔dla x≥
	2

	1
|1−2x|=|2x−1|=2x−1 dla x≥
	2

Widzisz na osi jak należy określić wyrażenia opuszczając znak wartości || f(x)=−2x+5+4(2x−1)=−2x+5+8x−4=6x+1

Agataku: czyli

	b		b
|ax−b|=ax−b dla ax−b≥0 ⇔x≥		lub |ax−b|=b−ax dla b−ax>0 ⇔x<
	a		a

	1		1
|1−2x|=1−2x dla 1−2x≥0 ⇔ x≤		lub |1−2x|=2x−1 dla 2x−1>0 ⇔x>
	2		2

jak rozumiem: zawsze nierownosc jest wieksza od zera [bo wartosc bezwzgledna wiec wiadomo] sa dwie mozliwosci jezeli nie zmieniamy znakow jest wieksza rowna "≥" od zera, a gdy zmieniamy to tylko wieksza ">" tak? [nastepnie oczywiscie oceniam ktora para nalezy do x∊(1,2) podkladam je pod rownanie, obliczam i koniec ]

Agataku: jezeli chodzi o znaki ≥ lub > to zalezy od tego czy zmieniamy czy przepisujemy z wartosci bezwzglednej tak? jezeli przepisujemy to ≥, jezeli zmieniamy znaki na przeciwne to > , to jest wazne chyba bo okresla czy dana liczba wlicza sie ...

Mila: znak "<"

Agataku: jak licze, nie wiem, juz mam pusto w glowie chyba, jak bylo |2x−5| to albo 2x−5≥0 ⇔x≥5/2 albo teraz na etapy jak ja to robilam −2x+5>0 ⇔ −2x>−5 |:(−2) ⇔ x<5/2 czyli nierownosc jest albo ≥ albo > tak?, x bedzie mial najwyzej znak < bo wyliczamy x a nie −x

Agataku: od 0

Agataku: jezeli bym zmienila znak −2x+5<0 ⇔ −2x <−5 ⇔ x>2/5 a tu sie nie zgadza z tym co mam w ksiazce i z tym co ci wychodzi wiec nierownosc powinna byc wieksza [lub rowna] albo to ja cos motam ale tak mi wychodzi

Agataku: x>5/2 * sorki moj blad

Mila: Nierówność: większy lub równy "≥0" albo nierówność: mniejszy "<0". Cały czas to Ci usiłuję wytłumaczyć, czy jesteś dysgrafką, czy popełniasz nieświadomie, czy świadomie błąd. AgatKO , najlepiej napisz swoje zadanie, będziemy wyjaśniać problemy.

Agataku: czyli popelnilam gafe

	5
wg rozwiazania w ksiazce −2x+5 dla x∊(−∞,		)
	2

[to jest ze zmienionym znakiem, wiec zgodnie z tym co piszesz: ] −2x+5<0 ⇔ −2x <−5 |:(−2)[dzielac przez minus obracam znak w przeciwna strone] ⇔ x>5/2 wiec przedzial by wygladal tak (5/2 ; +∞) a nie powinien, to mi tu nie pasuje, rozumiem co chcesz mi przekazac, znak przeciwny , ale dlaczego mi wychodzi inne rozwiazanie? tylko to mi tu nie pasuje, jezeli widzisz gdzies tu blad to wskaz mi go prosze

Mila:

	5
|2x−5|=2x−5 dla 2x−5≥0 ⇔x≥		"Część osi"
	2

	5
|2x−5|=−2x+5 dla 2x−5<0⇔x<		" reszta osi"
	2

Na tej samej zasadzie co dla liczb. |6|=6 |−6|=−(−6)=6

Agataku: jeszcze 20 minut temu dalabym sobie glowe obciac jezeli przy mnozeniu przez liczbe ujemna sie nie odwraca w przeciwna strone znaku nierownosci, teraz niczego nie jestem pewna

Agataku: aha czyli mimo iz zmieniamy znak, przepisujemy tak jak jest w wartosci bezwzglednej porownujac z zerem?

Mila: Agatko, mylisz dwie rzeczy. Jutro nad tym pomyśl. 3<6 /*(−2) −6>−12 zgadza się?

Agataku: to sie zgadza , glowa bylaby cala ale widzialas co liczylam, podstawiajac przeciwne znaki i co mi powychodzilo, sama liczac to samo [2x−5] bylo najpierw wieksze rowne, nastepnie mniejsze od 0 bez zmiany znakow w obu przypadkach ,

	5		5
2x−5≥0 lub 2x−5<0 ⇔ x≥		lub x<
	2		2

i tak sie by zgadzalo,przynajmniej wynikowo, w ten sposob powinno sie wyliczac przedzialy nalezace do x?

Aga1.: To jeszcze jeden przykład. I−x+5I=−x+5 , gdy −x+5≥0 teraz rozwiąż nierówność, czyli x≤5 tzn.x∊(−∞,5> I−x+5I=−(−x+5)=x−5 ,gdy −x+5<0, czyli x>5

Agataku: czyli Normalnie |2x−1|=2x−1 ⇔ 2x−1≥0 ⇔x≥¹₂ Zmiana znaku na przeciwny |2x−1| = 1−2x ⇔ 2x−1<0 ⇔x<¹₂

Mila: No widzisz, teraz dobrze.

Agataku: Mila dziekuje za poswiecony mi czas , musisz miec anielska cierpliwosc Wielkie dzięki Aga1. i Asia. dziekuje wam takze za pomoc

Mila: )