G Sorry .: Hej w jaki sposób mozna graficznie odjąć funkcje Czyli np |3x+6|−|2−x| jak mozna to zrobić graficznie ? Ps Wiem jakt to zrobić algebraivlcznie

Sorry .: jestem ciekawy w wolframe widać wyraźne podobieństwo pomiędzy wynikiem a pojedynczymi wykresami podanych funkcji

PW: Może to polegać na stwierdzeniu, że każda z tych funkcji jest "kawałkami liniowa", a wiec na "odpowiednich kawałkach osi" ich różnica jest też funkcją liniową, wtedy wystarcza wyznaczenie dwóch punktów wykresu. W tym przykładzie mamy do czynienia z trzema podzbiorami osi: (−∞,−2), [−2,2] i [2,∞). Różnica badanych funkcji ma wykres złożony z odcinka i dwóch półprostych. Wystarczy obliczyć wartości funkcji f(x) = |3x+6| − |2−x| dla x=−2 x= 2 i dwóch punktów leżących poza odcinkiem [−2,2].

Sorry . : Dzięki Interesuje mnie jednak wyznaczenie tej różnicy zaczynając od narysowana dwóch funkcji . Czy to możliwe?

PW: f(x) = 3|x+2| − |x−2| Na pewnych przedziałach mamy do czynienia z równoległymi półprostymi, a więc wskazanie różnicy jest proste, ale to tylko w takich szczególnych wypadkach. Odpowiedź wcześniejsza daje sposób uniwersalny.

Sorry . : Ok to jak narysować tą twoją funkcje ? Zapisz mi to proszę Wychodząc z wykresu funkcji y=x albo od razu y=x+2 ? Rozumiesz o co mi chodzi ?

Sorry: :€

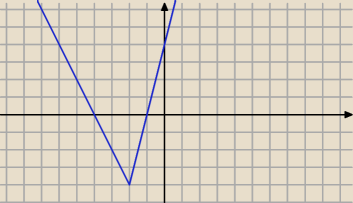
bezendu: Masz graficznie

Antek: bezendu popraw wykres bo narysowales zle Policz jak bedzie wygladal wzor funkcji w przedziale <−2 2) i potem w przedziale <2 nieskonczonosc )

bezendu: Antek narysowałem dobrze.

Antek: Skoro tak twierdzisz

bezendu: Niby czemu twierdzisz, że jest źle ?

Antek: Dlatego ze ten wykres wyglada tak jakby od x=−2 wykresem byla jedna linia prosta a to jest nieprawda . Dla przedzialu <−2,2) jest inny wykres i dla przedzialu < 2,nieskonczonosc ) wykresem jest inna linia prosta . O to mi chodzi ja sie moge kapnac ze braklo miejsca na wykresie na to zaznaczenie ale juz Sorry to troche watpie .

Antek: Przedzialy to moga byc roznie oznaczone np tak (−∞ −2> (−2 2) <2 ∞) byle tylko te przedzialy okreslay funkcje .

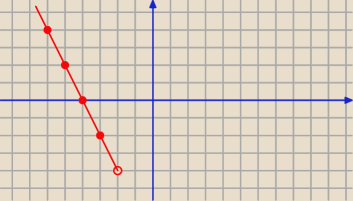
bezendu: f(x)=|3x+6|−|x−2| f(x)=3|x+2|−|x−2| 1⁰ (−∞,−2) 3(−x−2)−(−x+2) −3x−6+x−2 f(x)=−2x−8 dla x∊(−∞,−2) Będę rysował Ci w osobnych postach

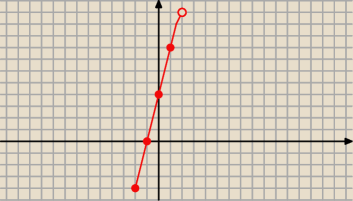
bezendu: f(x)=3|x+2|−|x−2| 2⁰ <−2,2) 3x+6−(−x+2) 3x+6+x−2 f(x)=4x+4 dla x∊<−2,2)

bezendu: f(x)=3|x+2|−|x−2| 3⁰ <2,∞) 3x+6−x+2 f(x)=2x+8 f(2)=12 Więc gdzie widzisz błąd ?

Antek: czy wykres funkcji y=4x+4 jest taki sam jak y=2x+8 ?

bezendu: Nie jest taki sam, po prostu dla funkcji f(x)=4x+4 12 nie należy do zbioru wartości a dla funkcji f(x)=2x+8 już tak (popatrz na przedziały) a po za tym funkcja f(x)=2x+8 przyjmuję duże wartości dla argumentów x∊<2.∞) i nie widać na wykresie

Sorry . : Dalej

Antek: Masz juz wszystko wyjasnione wiec zostalo tylko narysowac sobie w zeszycie

Sorry . : Jak narysowac ta funkcje za pomocą linijki i ołówka

Antek: Bedzie to taka funkcja f(x) ={−2x−8 dla x nalezy (−niesk. −2 ) {4x+4 dla x nalezy <−2,2) {2x+8 dla x nalezy (2, niesk ) Jak narysowac to za pomoca olowka i linijki ? 1. Bierzesz w reke olowek i za pomoca linijki rysujesz uklad wspolrzednych 2 zaznaczasz jednostki na osiach 3 Rysujesz za pomoca olowka i linijki wykresy tych funkcji ale nie cale tylko w tych przedzialach . tyle

Sorry . : Dzięki . Hhhhmmmmmm........