równanie z parametem ana: hej, pomożecie z takim zadankiem: wyznacz wszystkie wartości parametru m, dla których równanie|2x−2|/x+1=2m+3 ma dwa rozwiązania?

Bizon:

|2x−2|		|2x−2|
	+1 czy
x		x+1

ana: ta druga wersja

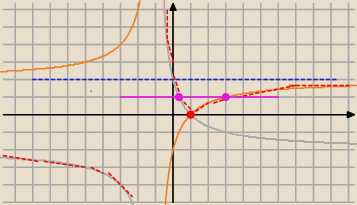Aga1.: Wykres lewej strony na czerwono.

	I2x−2		2x−2		2(x+1)−4		−4
		=		=		=		+2, gdy 2x−2≥0⇒x≥1
	x+1		x+1		x+1		x+1

	I2x−2I		−2x+2		−2(x+1)+4		4
i		=		=		=		−2, gdy x<1 i x≠−1
	x+1		x+1		x+1		x+1

Równanie ma 2 rozwiązania, gdy 0<2m+3<2 Rozwiąż.

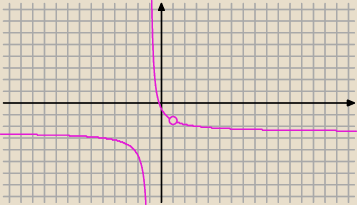Bizon: a) dla 2x−2<0 ⇒ 2x<2 ⇒ x<1

−2x+2
	=2m+3
x+1

−2(x+1)+4
	=2m+3
x+1

4
	−2=2m+3
x+1

4		2
	−5=2m ⇒		−2,5=m
x+1		x+1

b) dla x≥1 dla Ciebie potem wykresy i wnioski

ana: dzięki wielkie! po rozwiązaniu wyszło mi że m∊(−3/2,−1/2), czyli dokładnie tak jak w odpowiedziach