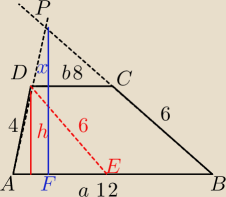
Trapez Messi: Dany jest trapez ABCD, którego podstawy mają długości : |AB|= 12, |CD|=8 a ramiona mają długości: |AD|=4 i |BC|=6. Ramiona przedłużono do przecięcia się w punkcie P. Oblicz pole trójkąta ABP. Sporządź rysunek. Prosze rozwiazanie

Messi: pilne!

Messi: !

messi: pomoz mi

Mila: |AE|=12−8=4 OBW_ΔAED=2*4+6=14 , p=7 − połowa obwodu P_ΔAED=√7*(7−6)*(7−4)²=√7*3²=3√7 ze wzoru Herona

	1
PΔAED=		*|AE|*h
	2

	1
3√7=		*4*h⇔3√7=2h
	2

	3√7
h=
	2

PF=H

	3√7
H=		+x
	2

ΔDCP∼ΔABP⇔odcinki jednego Δ są proporcjonalne do odpowiednich odcinków drugiego.

x		12
	=
8		1,5√7

Dokończysz?

messi: ne dokonczylem sie

Karol: to nie obliczylem sie o tym

Karol: czy to juz wszystko?

Mila: Ostatnie równanie źle przepisałam z kartki. Ma być:

x		H
	=
8		12

12x=8*H /:4 3x=2*H H=x+h 3x=2*(x+h) 3x=2x+2h x=2h

	3√7
x=		*2=3√7
	2

	3√7
H=3√7+
	2

H=4,5√7

	1
PΔABP=		*12*4,5√7
	2

P_ΔABP= 6*4,5√7= P_ΔABP= 27√7 Masz odpowiedź?

Karol: nie mam odpowiedz

Mila: Na koniec , pisze się" dziękuje" osobie pomagającej.