Prawdopodobieństwo
Vval: P(A') =
12 −−−> P(A) =
12
P(A∩B) =
13
P(A∪B) =
23
Oblicz P(B) ; P(A'∩B), P(A∩B')
23 =
12 + P(B) −
13
P(B) wychodzi
56
pytanie co zrobić z P(A'∩B) i P(A∩B') ?
Wpisuje dane do tego samego wzoru ( P(A∪B) = P(A) + P(B) − P(A∩B) ) tylko np. zamiast P(B)
wpisuje P(B') czyli
16 i mi wyjdzie P(A∩B')
Proszę o wskazówkę
Gustlik:
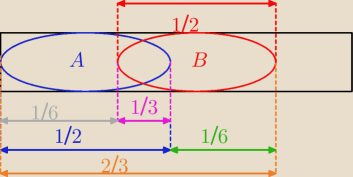
Zrób rysunek jak powyżej − to najlepszy graficzny sposób na tego typu zadania, nie potrzeba
znać wzorów, z rysunku można wszystko obliczyć.
| | 2 | | 1 | | 4 | | 3 | | 1 | |
P(A'∩B)= |
| − |
| = |
| − |
| = |
| |
| | 3 | | 2 | | 6 | | 6 | | 6 | |
| | 1 | | 1 | | 1 | | 2 | | 3 | | 1 | |
P(B)= |
| + |
| = |
| + |
| = |
| = |
| |
| | 6 | | 3 | | 6 | | 6 | | 6 | | 2 | |
| | 1 | | 1 | | 2 | | 1 | |
P(A∩B')= |
| − |
| =U{3{6}− |
| = |
| |
| | 2 | | 3 | | 6 | | 6 | |