Określ dziedzinę funkcji Geńjusz:

	1
y=√2+x−x2+
	√x2−3x

Dziedzina wg moich obliczeń to <−1,2>\{0} Może ktoś potwierdzić/zaprzeczyć?

Radek: −x²+x+2≥0 i x²−3x>0 to rozwiązałeś ?

Eta: D_f= <−1,0)

Geńjusz: Radek, tak, tylko wyszło mi inaczej niz Eta napisał/a. Moglibyście rozpisać to odrobinę?

Radek: Eta dobrze Ci napisała x²−3x>0 x(x−3)>0 x∊(−∞,0)∪(3,∞) −x²+x+2≥0 x²−x−2≤0 x∊<−1,2> część wspólna to <−1,0)

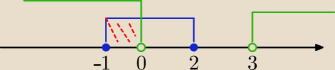
Eta: 1/ −x²+x+2≥0 /*(−1) x²−x−2≤0 (x−2)(x+1) ≤0 ⇒ x€ < −1,2> 2/ x²−3x>0 x(x−3)>0 ⇒ x€ (−∞ ,0) U (3,∞) teraz wybierasz część wspólną obydwu rozwiązać

Geńjusz: Ok, dzięki wielkie, już widzę swój błąd. To forum jest niezastąpione

Eta: Jasne że jest na zdrowie

Radek: Nie bierz tego

Eta: Radek

Radek: <robaczywka>

Eta: teraz dla Ciebie . ?

Radek: Oba poproszę I już przestałem liczyć Δ

Eta: Och Ty A już myślałam,że przez to liczenie wyróżnika ...... rozchorowałeś się

Radek: Zmieniłem nick na inny po prostu tamten był za długi ale bardzo fajny Pozdrawiam i dobranoc

Eta: Miłych snów

Geńjusz: yyyy jeszcze jedna funkcja

	x−2
y=log5
	x−5

Dziedzina to (5, +∞) ?

Aga1.:

x−2
	>0, x≠5
x−5

(x−2)(x−5)>0 x=2 v x=5 D=(−∞, 2)U(5,∞)