Oblicz objętość kuli
wajdzik:
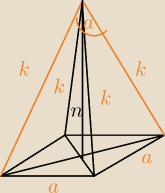
W prawidłowy ostrosłup czworokątny wpisano kulę. Oblicz objętość kuli wiedząc, że krawędź
podstawy ma długość a, natomiast kąt między przeciwległymi ścianami bocznymi ma miarę α.
n−wysokość
k−krawędź
a−krawędź podstawy
8 paź 20:20
wajdzik:
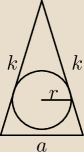
Wyjdzie nam trójkąt ramienny,
czy te rysunki są poprawne do treści zadania?
8 paź 20:21
wajdzik: 
8 paź 20:39
krystek: Kąt między przeciwległymi ścianami źle
8 paź 20:43
wajdzik:
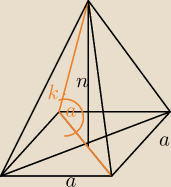
Teraz jest ok?
8 paź 21:17
matyk: Niestety źle
8 paź 21:18
Mila:
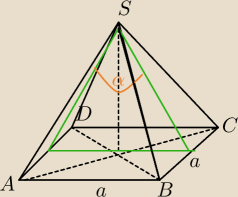
8 paź 21:51
matyk: Teraz ok

8 paź 22:00
wajdzik: dzięki Milu, staram się jak mogę ale za nic nie mogę się połapać w tych zadaniach.
8 paź 22:42
Mila:
Zrób kilka modeli szkieletowych i postaw na biurku.
Promień kuli wpisanej w ten ostrosłup jest równy promieniowi okręgu wpisanemu w zielony Δ.
Ta podpowiedź pomoże?
8 paź 23:31
dero2005:
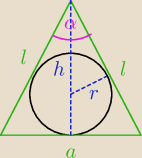
a
2 = 2l
2(1−cosα) ⇒ l =
h =
√l2 − (a2)2 =
9 paź 08:11
 W prawidłowy ostrosłup czworokątny wpisano kulę. Oblicz objętość kuli wiedząc, że krawędź
podstawy ma długość a, natomiast kąt między przeciwległymi ścianami bocznymi ma miarę α.
n−wysokość
k−krawędź
a−krawędź podstawy
W prawidłowy ostrosłup czworokątny wpisano kulę. Oblicz objętość kuli wiedząc, że krawędź
podstawy ma długość a, natomiast kąt między przeciwległymi ścianami bocznymi ma miarę α.
n−wysokość
k−krawędź
a−krawędź podstawy
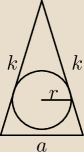 Wyjdzie nam trójkąt ramienny,
czy te rysunki są poprawne do treści zadania?
Wyjdzie nam trójkąt ramienny,
czy te rysunki są poprawne do treści zadania?

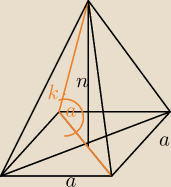 Teraz jest ok?
Teraz jest ok?


 a2 = 2l2(1−cosα) ⇒ l =
h = √l2 − (a2)2 =
a2 = 2l2(1−cosα) ⇒ l =
h = √l2 − (a2)2 =