Trapezz Beata: Zadanie domowe: Proszę bardzo o pomoc na jutro mam mieć zadanie domowe zrobione a już nie mam żadnych bz o to treść : Dany jest trapez równoramienny o podstawach długości √3, 5√3 i kącie ostrym 60 Oblicz pole trapezu: Czy w trapez ten można wpisać okrąg? Odpowiedź uzasadnij: Czy na trapezie tym można opisać okrąg? ___,,____ Bardzo proszę o pomoc Będę bardzo wdzięczna

AROB: pomagam

AROB:

	1
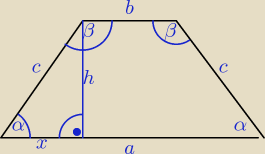
Dane: a = 5√3 P = ? P =		(a+b)*h
	2

b = √3 α = 60⁰

	a − b		5√3 − √3		4√3
x =		=		=		= 2√3
	2		2		2

	h
		= tgα
	x

	h
		= tg600
	3√3

h = 2√3 * √3 = 6

	1
P =		*(5√3 + √3) *6 = 6√3 * 3 = 18√3 [j2]
	2

W trapez (także w każdy czworokąt) można wpisać okrąg, gdy sumy długości przeciwległych boków są równe. Czyli musiałaby zachodzić równość: a + b = 2c Obliczamy c:

	h
		= sinα
	c

	6
		= sin600
	c

6		√3		12
	=		→ c =		= 4√3
c		2		√3

Sprawdzamy równość: a + b = 5√3 + √3 = 6√3 2c = 2 * 4√3 = 8√3 a + b ≠ 2c, czyli nie można wpisać okręgu w ten trapez. Okrąg można opisać na czworokącie, gdy suma miar kątów przeciwległych jest równa 180⁰. W trapezie β = 180⁰ − α = 120⁰ (z własności o sumie kątów przy jednym ramieniu). Zatem warunek ten jest spełniony i na tym trapezie można opisać okrąg.

Beata: Dziękuję Jesteś kochanyy