Algebra Garth: Zbadaj wlasnosci dzialania □ okreslonego w zbiorze R. x □ y := ³√x³ + y³ I wlasciwie chodzi mi tylko o lacznosc, bo z reszta sobie poradzilem. (a □ b) □ c = (³√a³ + b³ □ c = ³√³√a³ + b³' + c³ = ...? a □ (b □ c) = a □ (³√b³ + c³) = ³√a³ + ³√b³ + c³' = ...? W obu przypadkach mala kreseczka u gory zaznaczylem, gdzie sie konczy wewnetrzny pierwiastek. Na pierwszy rzut oka wygladaja na rozne, ale w odp. jest, ze dzialanie jest laczne, wiec powinno wyjsc to samo, a nie bardzo mam pomysl na przeksztalcenie...moze szescian sumy albo suma szescianow?

Garth: I z innej beczki − jak narysowac |x| < |y|? Jeszcze narysowanie |x| to dla mnie nie problem, ale |y| juz tak [wydawalo mi sie, ze bedzie to wykres |x| odwrocony o 90 stopni w prawo, ale tak nie jest ].

Basia: wystarczy podać kontrprzykład x = ³√³√a³+b³+c³ y = ³√a³+³√b³+c³ a=1 b=2 c=3 x = ³√³√1+8+27 = ³√³√9+27 y = ³√1+³√8+27 = ³√1+³√35 x³ = ³√9+27 > 0+27=27 y³ = 1 + ³√35 < 1+4=5 skoro x³≠y³ ⇒ x≠y

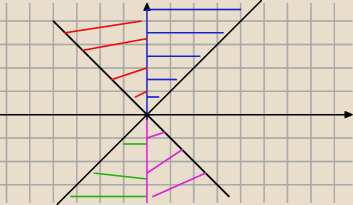
Basia: I ćwiartka (x≥0 i y≥0): x<y II ćwiartka (x<0 i y>0): −x < y III ćwiartka (x<0 i y<0): −x<−y ⇔ x>y IV ćwiartka (x≥0 i y<0): x < −y −x>y i oczywiście to jest suma

Garth: Dziekuje, wiec wychodzi na to, ze jednak to moje dzialanie nie bylo laczne...

Garth: a ▱ b := a^b; okreslone w zbiorze R₊ Laczne?

Garth: (a ▱ b) ▱ c = (a^b) ▱ c = a^bc a ▱ (b ▱ c) = a ▱ (b^c) = (a)^bc ?

Basia: (2□3)□2 = (2³)□2 = 8□2 = 8² = 64 2□(3□2) = 2□(3²) = 2□9 = 2⁹ = 512 a^bc ≠ a^b*c

Basia: (a^b)^c = a^b*c a^bc = a^(bc) ≠ a^b*c

Garth: Dzieki, ale chyba oba przypadki nazywaja sie potega potegi? Czy maja jakies rozne nazwy?

Basia: nic mi o różnych nazwach nie wiadomo; przyjęto konwencję, że w zapisie a^bc najpierw wykonujemy b^c a dopiero potem a^wyniku