:) PuRXUTM: Witam Mam pytanie czy polecenie zbadaj injektywność funkcji (albo iniektywność bo nie wiem jak jest poprawnie) to oznacza dokładnie to samo co zbadaj czy funkcja jest różnowartościowa ? i jeszcze jedno mam f(1−x) czyli to jest inaczej f(−(x−1)) czyli mam pierwsze przesunąć o jeden w prawo a później symetria względem osi OY tak ?

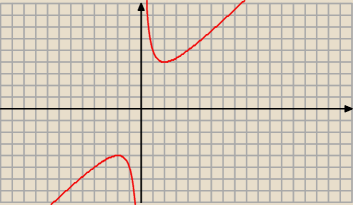asdf: jaka to funkcja? ty chcesz udowodnic roznowartosciowosc za pomoca nieparzystości?, np.

	x2+4
f(x) =		jest nieparzysta, ale roznowartościowa.
	x

Roznowartosciowosc mozna za pomoca pochodnych dowodzic, ale nie za pomoca funkcji parzystej / nieparzystej.

asdf: sorry..zle przeczytalem do pierwszego: http://pl.wikipedia.org/wiki/Injekcja do drugiego: "mam f(1−x) czyli to jest inaczej f(−(x−1))" − tak nie jest..

PuRXUTM: a jak jest ? bo z tego co kojarze ze szkoły to tak nas chyba uczyli

asdf: zakladasz, ze f(1−x) = f(x−1) niech: δ = 1 − x f(δ) = f(−δ) dajmy funkcję: f(δ) = 2*δ, dla δ = 1: f(1) = 2, f(−1) = −2 ⇒ f(1) = f(−1) ⇒ −2 = 2 fałsz ale dla funkcji: f(δ) = δ², dla δ = 1: f(1) = 1; f(−1) = (−1)² = 1 ⇒ f(1) = f(−1) ⇒ 1 = 1 prawda Zalezy jaka masz funkcje..ale jak nie chcesz jej podac to jak ma CI ktokolwiek pomoc

PuRXUTM: mam takie zadanie, sory że nie napisałem na początku Niech f(x)=(x−3)(2x+1), x∊R narysuj x→f(1−x)

asdf: spoko, to teraz narysuj: no to za x wstaw 1−x:

	3
f(1−x) = (1−x − 3)(2(1−x) + 1) = −(x+2)(−2x + 3) = (x+2)(2x−3) = 2*(x+2)(x −		)
	2

PuRXUTM: asdf, wiesz chodzi mi raczej o takie ogólne przekształcenie tego f(1−x) bo jestem na studiach Jak byś mógł mam jeszcze jedno pytanie mam takie coś (mniejsza o treść zadania )

	π		5π
(2x−1) ∊[2kπ;		+2kπ] U [		+2kπ;2π+2kπ]
	6		6

mam wyliczyć x

	π		5π
2x ∊[2kπ+1;		+2kπ+1] U [		+2kπ+1;2π+2kπ+1]
	6		6

	π		5π
x ∊[kπ+0,5;		+kπ+0,5] U [		+kπ+0,5;π+kπ+0,5 dobrze ?
	12		12

PuRXUTM: up

PuRXUTM: up

PuRXUTM: up

Mila: 16:17, wydaje mi się, że dobrze. Zad1. f(1−x)= f(x)→S_OY→f(−x)→T[1,0]→f(−(x−1))+0=f(−x+1) Przykład. f(x)=x+2 spr. rachunkowo: f(1−x)=(1−x)+2=−x+3 I sposób (najpierw symetria) f(x)→S_OY→f(−x)=−x+2→T[1,0]→g(x)=−(x−1)+2=−x+1+2=−x+3 II sposób ( najpierw translacja T[1,0] f(x)=x+2→T[1,0]→f(x−1)=x−1+2=x+1→S_x=1→−x+3 III sposób ( najpierw translacja T[−1,0] f(x)=x+2→T[−1,0]→(x+1)+2=x+3→S_OY→g(x)=−x+3

PuRXUTM: dzięki wielkie Milu ! Jesteś nieoceniona !

asdf: Przepraszam, nie było mnie − z uczelni dopiero wróciłem

Mila:

PuRXUTM: nie masz za co przepraszać Cieszę się że poświęciłeś mi swój czas kurde boje się że wylecę z tych studiów... zaczyna się ciekawie...

Mila: Nie panikuj, pracuj, pożycz z Jagiellonki dobre książki, kup zbiory zadań. Czytaj, czytaj literaturę, porozmawiaj z rozsądnymi kolegami z II roku.

PuRXUTM: ehhh dobra no to kolejne zadanko Zbadaj iniektywność funkcji α:(−π;3π]∍x→sin(4x−1) ∊R

asdf: chyba będzie to przedział: (sin(−4π − 1);sin(12π−1)] = (sin(−1);sin(−1)] czyli jest to punkt. Tak mi się wydaje

asdf: nie...to nie będzie punkt. Co ja piszę Jedynie to przyjmie on wartości takie, że: sin(−4π−1) = sin(−2π−1) = sin(−1) = ...wniosek?