wektory zadanie: dane sa wektory a=[1,0], b=[1,1] i c[−1,0] rozloz wektor b wzgledem a i c oraz rozloz wektor a wzgledem b i c prosze o pomoc

zadanie: ?

zadanie: ?

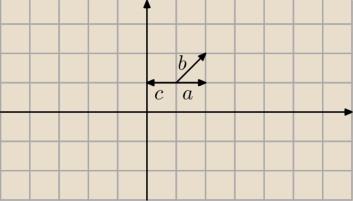
Mila: Każdy wektor w^→ na płaszczyźnie można przedstawić w postaci: w^→=m*u^→+n*v^→ gdzie wektory u i v nie są równoległe, m,n∊R

zadanie: dziekuje czyli a) wektor b wzgledem a i c nie mozna bo te wektory sa rownolegle b) mam jeszcze takie pytanie czy jezeli powiem, ze wektory sa liniowo zalezne, wspolliniowe, rownolegle, maja te same kierunki to czy to jest to samo?

Mila: Tak. Posprawdzaj definicje na wykładzie. To z geometrii zadanie? wektor a masz rozłożony?

zadanie: wektory b i c nie sa rownolegle wiec moge rozlozyc wektor a wzgledem b i c a=t₁b+t₂c [1,0]=t₁[1,1]+t₂[−1,0]=[t₁,t₁+[−t₂,0]=[t₁−t₂,t₁] t₁−t₂=1 t₁=0 stad t₁=0 t₂=−1 szukany rozklad: [1,0]=0*[1,1]+(−1)*[−1,0] dobrze?

zadanie: mam jeszcze 2 zadania 2. uzasadnij za pomoca rachunku we wspolrzednych obydwie wlasnosci rozdzielnosci mnozenia wzgledem dodawania dla wektorow i liczb. tego nie potrafie 3. znajdz katy biegunowe wektorow: a) [1,−1] b) [−3,3] c) [0,−4] d) [2,0] dwoma sposobami 1) odczytujac wartosc odpowiedniego kata z rysunku oraz 2) wyliczajac sinus i cosinus tego kata ze wspolrzednych wektora a) 1) na rysunku ten kat znajduje sie w czwartej cwiartce (odczytac moge za pomoca katomierza) 2) dlugosc tego wektora to √2

	1		√2
cosα=		=
	√2		2

	−1		√2
sinα=		=−
	√2		2

stad jezeli ten kat znajduje sie w czwartej cwiartce to α=270^o+45^o=315^o 45^o bo dla takiego kata cosinus przyjmuje taka wartosc pozostale przyklady podobnie dobrze?

zadanie: prosilbym o pomoc

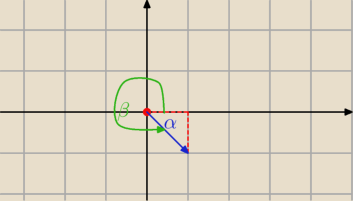
Mila: 1) Nie kątomierzem! ( zapomnij o nim) Układ jest prostokątny. Masz tam przekątną kwadratu. α=−45^o β=360−45=315

Mila: Resztę później.

zadanie: dobrze dziekuje

Mila: Zapisz dokładnie treść 2 zadania. Jakie miałeś podane własności na wykładzie.

zadanie: tresc taka jak wyzej a wlasnosci takie t(v+w)=tv+tw (t+s)v=tv+sv

Mila: Dla k∊R,a^→[a₁a₂] i b^→[b₁,b₂] wiemy że dla k∊R: (1) k*[x,y]=[kx,ky] Zatem: k*(a^→+b^→)=k*a^→+k*b^→ k*([a₁,a₂] +[b₁,b₂])= dodajemy w nawiasie odpowiednie współrzędne wektorów =k*[a₁+b₁,a₂+b₂]= korzystamy z (1) =[k*a₁+k*b₁,k*a₂+k*b₂]= =[k*a₁,k*a₂]+[k*b₁,k*b₂]=k*[a₁,a₂]+k*[b₁,b₂]

Mila: Mam nadzieję,że nie ma pomyłki, bo ciągle muszę odchodzić od komputera.

zadanie: dziekuje

Mila: