Funkcja
bezendu:
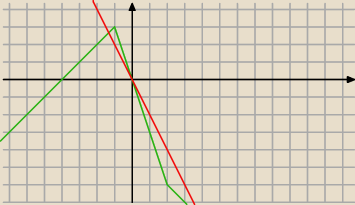
Naszkicuj wykres funkcji f(x)=
√4−4x+x2−2
√x2+2x+1. Korzystając z wykresu funkcji f określ
liczbę rozwiązań równania f(x)=−2x+b w zależności od parametru b
f(x)=|x−2|−2|x+1|
1
0 (−
∞,−1)
−x+2+2x+2
x+4
2
0 <−1,2)
−x+2−2x−2
−3x
3
0 <2,
∞)
x−2−2x−2
−x−4
b∊(1,
∞) brak rozwiązań
b{1} jedno rozwiązanie
Ale jak dalej ?
7 paź 23:41
Mila: Dzisiaj, Dobranoc. Idź spać.
Jutro pracujemy systematycznie.
7 paź 23:43
bezendu:
Dobrze. To do jutra


7 paź 23:46
Mila:
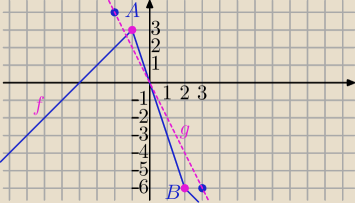
f(x)=|x−2|−2|x+1|
g(x)=−2x+b
1) x<−1
f(x)=x+4
2) x∊<−1,2)
f(x)=−3x
3) x≥2
f(x)=−x−4
a) Zauważ,że prosta g (odpowiednio przesunięta równolegle) przecina wykres jednym punkcie gdy
znajduje się poniżej punktu B=(2,−6) i powyżej punktu A=(−1,3)
Zatem sprawdzamy:
g(2)=−2*2+b=−6⇔b=−2
g(−1)=−2*(−1)+b=3⇔b=1
stąd jedno rozwiązanie dla b>1 lub b<−2
b) Dla b=1 prosta przecina część wykresu f(x)=−x−4 i przechodzi przez punkt A
Dla b=−2 prosta przecina część wykresu f(x)=x+4 i przechodzi przez punkt B⇔
Dwa rozwiązania dla b∊{1,−2}
c) Prosta g poruszając się równolegle od punkt B do A przecina trzy gałązki wykresu f(x) ⇔
dla b∊(−2,1) równanie ma trzy rozwiązania.
To dość trudne, ale pomocniczo rozwiązałabym takie równanie;
|x−2|−2|x+1|=−2x+b⇔
I to będzie w następnym wpisie.
8 paź 18:28
Mila:
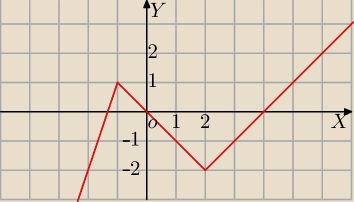
To dość trudny sposób zaproponowany w zadaniu, ale rozwiązałabym łatwiejsze równanie
równoważne;
|x−2|−2|x+1|=−2x+b⇔
|x−2|−2|x+1|+2x=b⇔
h(x)=|x−2|−2|x+1|+2x
1) x<−1
h(x)=x+4+2x=3x+4
2) x∊<−1,2)
h(x)=−3x+2x=−x
3) x≥2
h(x)=−x−4+2x=x−4
h(x)=b
Dla b∊(−
∞,−2)∪(1,
∞) jedno rozwiązanie
Dla b∊{−2,1} dwa rozwiązania
Dla b∊(−2,1) trzy rozwiązania
8 paź 18:36
bezendu:
Mila czumu rozwiązujesz dodatkowo to równanie ?
8 paź 18:37
Mila:
Rozwiązałam innym sposobem, aby Ci pokazać, że łatwiej ustalić, ile rozwiązań ma równanie w
zależności od parametru b.
8 paź 18:47
bezendu:
Pomysł z dodatkowym równaniem jest świetny, tylko szkoda,że ja na to nie wpadłem...
8 paź 19:34
matyk: zawsze warto tak robić żeby parametr był po prawej stronie. Wtedy graficznie się ładnie
rozwiązuje

8 paź 19:37
 Naszkicuj wykres funkcji f(x)=√4−4x+x2−2√x2+2x+1. Korzystając z wykresu funkcji f określ
liczbę rozwiązań równania f(x)=−2x+b w zależności od parametru b
f(x)=|x−2|−2|x+1|
10 (−∞,−1)
−x+2+2x+2
x+4
20 <−1,2)
−x+2−2x−2
−3x
30 <2,∞)
x−2−2x−2
−x−4
b∊(1,∞) brak rozwiązań
b{1} jedno rozwiązanie
Ale jak dalej ?
Naszkicuj wykres funkcji f(x)=√4−4x+x2−2√x2+2x+1. Korzystając z wykresu funkcji f określ
liczbę rozwiązań równania f(x)=−2x+b w zależności od parametru b
f(x)=|x−2|−2|x+1|
10 (−∞,−1)
−x+2+2x+2
x+4
20 <−1,2)
−x+2−2x−2
−3x
30 <2,∞)
x−2−2x−2
−x−4
b∊(1,∞) brak rozwiązań
b{1} jedno rozwiązanie
Ale jak dalej ?


 f(x)=|x−2|−2|x+1|
g(x)=−2x+b
1) x<−1
f(x)=x+4
2) x∊<−1,2)
f(x)=−3x
3) x≥2
f(x)=−x−4
a) Zauważ,że prosta g (odpowiednio przesunięta równolegle) przecina wykres jednym punkcie gdy
znajduje się poniżej punktu B=(2,−6) i powyżej punktu A=(−1,3)
Zatem sprawdzamy:
g(2)=−2*2+b=−6⇔b=−2
g(−1)=−2*(−1)+b=3⇔b=1
stąd jedno rozwiązanie dla b>1 lub b<−2
b) Dla b=1 prosta przecina część wykresu f(x)=−x−4 i przechodzi przez punkt A
Dla b=−2 prosta przecina część wykresu f(x)=x+4 i przechodzi przez punkt B⇔
Dwa rozwiązania dla b∊{1,−2}
c) Prosta g poruszając się równolegle od punkt B do A przecina trzy gałązki wykresu f(x) ⇔
dla b∊(−2,1) równanie ma trzy rozwiązania.
To dość trudne, ale pomocniczo rozwiązałabym takie równanie;
|x−2|−2|x+1|=−2x+b⇔
I to będzie w następnym wpisie.
f(x)=|x−2|−2|x+1|
g(x)=−2x+b
1) x<−1
f(x)=x+4
2) x∊<−1,2)
f(x)=−3x
3) x≥2
f(x)=−x−4
a) Zauważ,że prosta g (odpowiednio przesunięta równolegle) przecina wykres jednym punkcie gdy
znajduje się poniżej punktu B=(2,−6) i powyżej punktu A=(−1,3)
Zatem sprawdzamy:
g(2)=−2*2+b=−6⇔b=−2
g(−1)=−2*(−1)+b=3⇔b=1
stąd jedno rozwiązanie dla b>1 lub b<−2
b) Dla b=1 prosta przecina część wykresu f(x)=−x−4 i przechodzi przez punkt A
Dla b=−2 prosta przecina część wykresu f(x)=x+4 i przechodzi przez punkt B⇔
Dwa rozwiązania dla b∊{1,−2}
c) Prosta g poruszając się równolegle od punkt B do A przecina trzy gałązki wykresu f(x) ⇔
dla b∊(−2,1) równanie ma trzy rozwiązania.
To dość trudne, ale pomocniczo rozwiązałabym takie równanie;
|x−2|−2|x+1|=−2x+b⇔
I to będzie w następnym wpisie.
 To dość trudny sposób zaproponowany w zadaniu, ale rozwiązałabym łatwiejsze równanie
równoważne;
|x−2|−2|x+1|=−2x+b⇔
|x−2|−2|x+1|+2x=b⇔
h(x)=|x−2|−2|x+1|+2x
1) x<−1
h(x)=x+4+2x=3x+4
2) x∊<−1,2)
h(x)=−3x+2x=−x
3) x≥2
h(x)=−x−4+2x=x−4
h(x)=b
Dla b∊(−∞,−2)∪(1,∞) jedno rozwiązanie
Dla b∊{−2,1} dwa rozwiązania
Dla b∊(−2,1) trzy rozwiązania
To dość trudny sposób zaproponowany w zadaniu, ale rozwiązałabym łatwiejsze równanie
równoważne;
|x−2|−2|x+1|=−2x+b⇔
|x−2|−2|x+1|+2x=b⇔
h(x)=|x−2|−2|x+1|+2x
1) x<−1
h(x)=x+4+2x=3x+4
2) x∊<−1,2)
h(x)=−3x+2x=−x
3) x≥2
h(x)=−x−4+2x=x−4
h(x)=b
Dla b∊(−∞,−2)∪(1,∞) jedno rozwiązanie
Dla b∊{−2,1} dwa rozwiązania
Dla b∊(−2,1) trzy rozwiązania
