Funkcja bezendu: Mila Czy mogłabyś wyprowadzić mi wzór na przesunięcie wykresu funkcji (obojętnie jakiej) w symetrii względem a) x=−1 b) x=5 c) y=−5 d) y=4

Saizou : a po co ci to?

Trivial: bezendu, a czemu nie możesz sam wyprowadzić?

bezendu: Żeby przekształcać wykresy funkcji Mogę ale, nie wiem czy zrobię to dobrze, dlatego proszę o pomoc

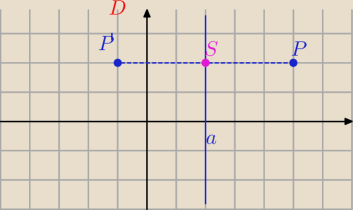
Mila: Tak, to się nazywa przekształcenie wykresu funkcji przez symetrię osiową. a) symetria względem prostej: x=a P(x,y) dany punkt P'(x',y') =S_x=a(P(x,y)) Punkt P' jest symetryczny do punktu P względem prostej x=a S=(a,y) środek odcinka PP'

	x+x'
a=		⇔x+x'=2a⇔x'=2a−x
	2

	y+y'
y=		⇔2y=y+y'⇔y'=y
	2

Przekształcenie określają wzory: x'=2a−x y'=y dla x=−1 będzie x'=2*(−1)−x⇔x'=−2−x y'=y dla x=5 x'=2*5−x⇔x'=10−x y'=y Przykład z funkcją będzie w następnym wpisie.

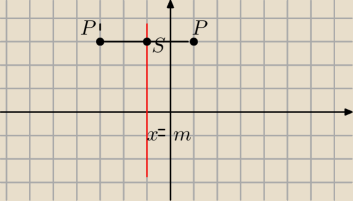
Aga1.: P(x,y) P(x^',y^') S(m,y) {x+x^'}{2}=m⇒x^'=2m−x y^'=y

Mila: 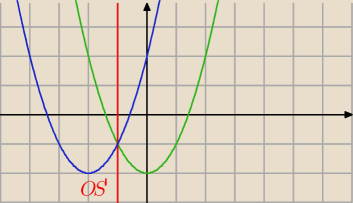dla x=−1 x'=−2−x y'=y f(x)=y=x²−2, x'=−2−x⇔x=−2−x' y'=(−2−x')²−2 y'=4+4x'+x'²−2 y'=x'²+4x'+2 opuszczamy znaczki ' y=x²+4x+2 wzór funkcji po przekształceniu przez symetrię względem prostej x=−1 wykresu funkcji f(x)=y=x²−2 W podobny sposób wyprowadzasz wzory na symetrię osiową względem prostej y=a, a∊R Czy poradzisz sobie? Sprawdzę.

Mila: Czy o to Ci chodziło?

bezendu: Dziękuję Tak chodziło mi dokładnie o to Kiedyś już wyprowadzałaś mi wzór na przekształcenie ale zgubiłem link.

bezendu: Jeszcze jedno pytanie: Czy na poziomie lo jest przekształcenie wykresu względem prostej y=−2x+7 ? Pytam się bo mam kartkówkę niedługo z przekształcania wykresów funkcji.

Mila: Nie powinno być. Napisz jakie masz zadania z przekształceń.

bezendu: Np. wykres funkcji f(x)=x³+3x+2 przekształcono a) względem prostej x=2 b) względem prostej y=−2 c) względem początku układu współrzędnych I dlatego moje pytanie odnośnie przekształceń

bezendu: Jeszcze mam zadani odnośnie narysuj wykres i określ liczbę rozwiązań w zależności od parametru. W nowym wątku wstawię zadanie do sprawdzenia.

Mila: post 23:29 Masz podać wzory funkcji po przekształceniu wykresu?

Mila: Napisz co obliczyłeś, najpierw wzory x'=... y'=... potem wzór nowej funkcji.

Mila: Może jutro, teraz idź spać, bo nie wstaniesz do szkoły.

bezendu: Chodzę spać po 02:00 Odnośnie pytania to tak,mam podać wzory po przekształceniu.

Mila: Wpisz ,jutro sprawdzę. DOBRANOC

bezendu: c) względem początku układu wsp f(x)=x³+3x+2 −f(−x)=−[(−x)³+3(−x)+2] −f(−x)=−[−x³−3x+2] −f(−x)=x³+3x−2

bezendu: Dobranoc

Mila: c) dobrze Powinieneś jeszcze umieć wyprowadzić wzory dla symetrii względem prostej y=x ( to ważne). Czekam na Twoje rozwiązanie Wykres funkcji f(x)=x³+3x+2 przekształcono a) względem prostej x=2 b) względem prostej y=−2

bezendu: Teraz idę na kolację. Za 15 minut wracam z rozwiązaniem

bezendu: f(x)=x³+3x+2 a) względem prostej x=2 Czyli post 22:30 tak ?

Mila: Tam było względem prostej x=−1 i masz wzór,skorzystaj, nie wyprowadzaj go, bo to już umiesz. Wyprowadź wzór na przekształcenie przez symetrię względem Oy i prostej y=x.

Mila: Teraz ja też idę na kolację, którą muszę przyrządzić.

bezendu: 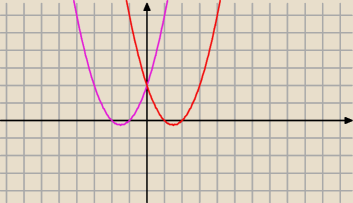Mila względem osi Oy to mam f(−x) np. x²+3x+2 względem osi Oy f(−x)=(−x)²−3x+2 f(−x)=x²−3x+2

Mila: Dalej, gd\zie reszta? Mój post.18:52

bezendu: Nie wiem jak przesunąć względem y=−2 czy mogę przesunąć to jakoś o wektor ?

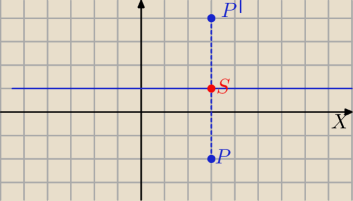
Mila: Nie przesunąć lecz odbicie symetryczne masz w zadaniu. Symetria względem prostej y=a, a∊R P=(x,y) P'=(x',y') obraz punktu P w symetrii względem prostej y=a (S_y=a)

matyk: W ogóle takich przekształceń nie ma na poziomie lo w żadnej podstawie obecnie

bezendu:

	x+2
A mogę prosić na konkretnym przykładzie np f(x)=		? Bo nie za bardzo wiem jak
	x2+2x+1

się za to zabrać..

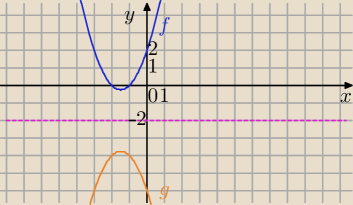
Mila: cd. za wcześnie wysłałam. S=(x,a) jest środkiem odcinka PP'

	x+x'
x=		⇔2x=x+x'⇔x'=x
	2

	y+y'
a=		⇔y+y'=2a⇔y'=2a−y
	2

Obrazem punktu P(x,y) w symetrii względem prostej y=a jest taki punkt P'(x',y'), że x'=x y'=2a−y Przykład: f(x)= x²+3x+2 y=−2 oś symetrii x'=x y'=2*(−2)−y⇔y'=−4−y⇔y=−4−y' podstawiam do wzoru: y=x²+3x+2 −4−y'=x'²+3x'+2⇔−y'=x'²+3x'+2+4 −y'=x'²+3x'+6 y'=−x'²−3x'−6 g(x)=y=−x²−3x−6

Mila: 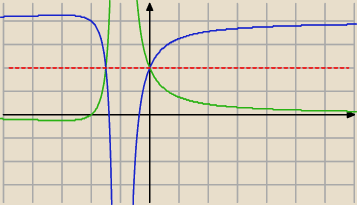Obrazem punktu P(x,y) w symetrii względem prostej y=a jest taki punkt P'(x',y'), że x'=x y'=2a−y Względem prostej y=2 x'=x y'=4−y

	x+2
f(x)=y=
	(x2+2x+1)

	x'+2
4−y'=
	x'2+2x'+1)

	x'+2
−y'=		−4
	(x'2+2x'+1)

	x'+2		4*(x'2+2x'+1)
−y'=		−
	(x'2+2x'+1)		(x'2+2x'+1)

	x'+2−4x'2−8x'−4
−y'=
	x'2+2x'+1

	4x2+7x+2
y=
	(x+1)2

bezendu: Mila ja już dziś muszę kończyć. Jutro wrzucę kilka przykładów do sprawdzenia P.S Świetnie tłumaczysz Dziękuję

Mila: