różnowartościowość funkcji Ania: sprawdź czy funkcja jest różnowartościowa. f(x)= 4x − 5 może mi ktoś wytłumaczyć jak to się sprawdza?

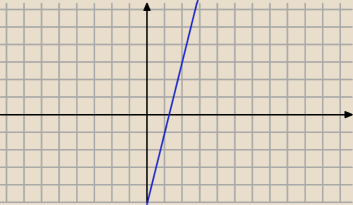
bezendu: Funkcja jest różnowartościowa

Piotr 10: Założenie: x₁≠x₂ ⋀ D=R ⋀ x₁−x₂≠0 Teza: f(x₁)≠f(x₂) Dowód: f(x₁)−f(x₂)=4x₁−5 − (4x₂−5)=4x₁−5−4x₂+5 4(x₁−x₂)≠0 4≠0 x₁−x₂≠0 ( z założenia) c.n.u

Aleksandra: dzięk i a mógłbyś mi powiedziec jak to się sprawdza algebraicznie?

bezendu: Patrz post Piotra

Piotr 10: Witaj bezendu

Aleksandra: już widzę dzięki Wam

bezendu: Cześć Piotrek

Aleksandra: a możecie mi jeszcze wytłumaczyć kiedy jest możliwe złożenie funkcji? Będę bardzo wdzięczna

Aleksandra: pomozecie?