Punkty A(-1,5) oraz B(3,3) są symetryczne względem prostej k. Wyznacz równanie p GOGA: Punkty A(−1,5) oraz B(3,3) są symetryczne względem prostej k. Wyznacz równanie prostej k. Proszę o obliczenia !

Piotr 10: Hmm, możesz zrobić to tak, napisz równanie przechodzące przez dwa punkty A i B Szukana prosta k jest prostopadła do prostej AB Wyznacz też środek AB Lub też wektorowo A*(x−x_o)+B*(y−y₀)=0 Wylicz wektor AB^→ I środek AB

Mila: Prosta k jest symetralną odcina AB. Symetralna odcinka to zbiór wszystkich punktów jednakowo odległych od końców odcinka. P(x,y) − punkt należacy do symetralnej AB. √(x+1)²+(y−5)²=√(x−3)²+(y−3)² /² x²+2x+1+y²−10y+25=x²−6x+9+y²−6y+9 dokończ.

GOGA: ,aa nie rozumiem nie mogę wyznaczyc prostej AB bo nie wiem w jakim punkcie przecina os OY, a drugiego rozwiązania Mili to wogóle nie łapie

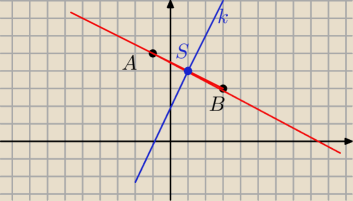
Aga1.: Szukana prosta k jest prostopadła do prostej AB i przechodzi przez środek odcinka AB. 1) Wyznacz S środek odcinka AB. S(1,4) 2) Wyznacz a₁ współczynnik kierunkowy prostej AB( nie musisz liczyć b) a₁= 3) Korzystając z warunku prostopadłości prostych napisz równanie prostej k.

Gustlik: Zrób jak proponuje Ci Aga1, a współczynnik kierunkowy możesz obliczyć z wektorów. AB^→=[x_B−x_A, y_B−y_A], podziel potem współrzedną "y" wektora AB przez współrzedną "x" i masz współczynnik kierunkowy.