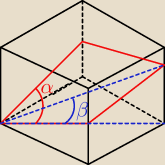
Przekrój graniastosłupa prawidłowego czworokątnego płaszczyzną przechodzącą przez jeden z
wierzchołków dolnej podstawy jest rombem o kącie α. Oblicz cosinus kąta β nachylenia tego
przekroju do płaszczyzny dolnej podstawy
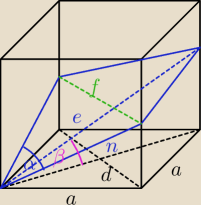oznaczenia:
a − krawędź podstawy graniastosłupa
d − przekątna podstawy graniastosłupa
n − bok rombu
e − przekątna dłuższa rombu
f − przekątna krótsza rombu
d = a√2
d = f = a√2
f2 = 2n2(1 − cosα)
| f2 | 2a2 | |||
2n2 = | = | |||
| (1 − cosα) | 1−cosα |
| e*f | ||
Pr = n2sinα = | ||
| 2 |
| 2n2sinα | ||
e = | ||
| a√2 |
| 2a2sinα | ||
e = | ||
| a√2(1−cosα) |
| d | 1−cosα | |||
cosβ = | = | |||
| e | sinα |
